na czym polegało znaczenie powstania wielkopolskiego??

Zaproszenie

Przykładowe rozwiązanie zadania:

I would like to invite you to an ending party of Black Swan Club. It's going to be our last meeting so we have decided to make a party out of it. Furthermore, it's also going to be one of my last days here in Coventry so it would be a nice way to say goodbye to you all.

Black Swan Club was a great experience for me. I chose it because of large variety of artistic programme.

During the party there is going to be a competition. We are going to read things about each of us and your task will be to guess who it is about.  There will be a price for a winner!

The event will take place at the school, so getting there will probably not be a problem. Also, there will be a bus every hour that you can use to get to the event.

Zaproszenie (invitation) - jest to forma krótkiego tekstu użytkowego, poprzez którą zaprasza się pewną osobę lub grupę osób na wydarzenie (mogą być to urodziny, imieniny ślub lub także premiery filmów, wystawy, wernisaże itp).

W zaproszeniu należy zawrzeć:

• formułę zapraszającą uczestników na dane wydarzenie, przykładowe zwroty: I would like to invite you; I would be honoured if you would come; I am organising; You're all invited; There will be held.
• powód, dlaczego organizuje sie dane wydarzenie (a jeśli chce się zachęcić kogoś do przyjścia to warto też napisać dlaczego warto przyjść)
• podać czas i miejsce wydarzenia

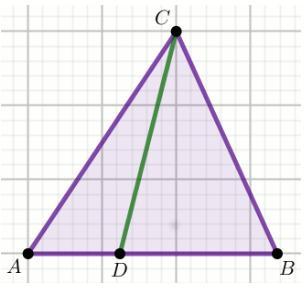
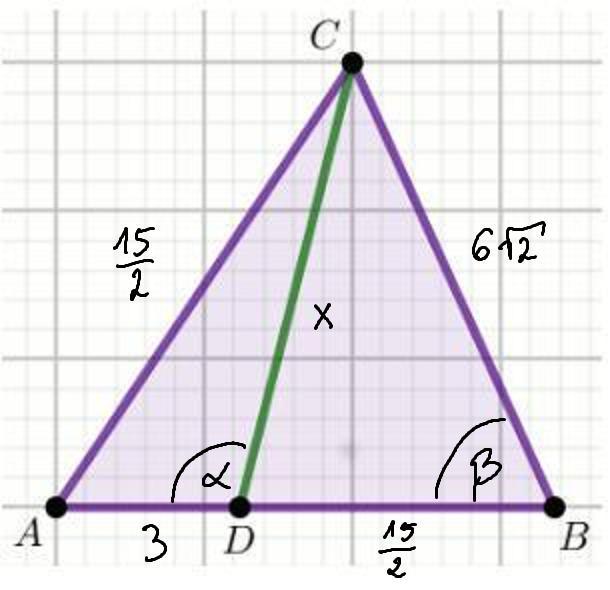
Dodatkowe dane zaznaczone na rysunku.

Tw. cosinusów

[tex]a^2=b^2+c^2-2bc\cos\alpha[/tex]

Obliczenie cosinusa kąta β:

[tex]|AB|=3+\dfrac{15}{2}=\dfrac{6}{2}+\dfrac{15}{2}=\dfrac{21}{2}[/tex]

[tex]|AC|^2=|AB|^2+|BC|^2-2|AB||BC|\cos\beta\\\left(\dfrac{15}{2}\right)^2=\left(\dfrac{21}{2}\right)^2+\left(6\sqrt{2}\right)^2-2\cdot\dfrac{21}{2}\cdot6\sqrt{2}\cos\beta\\\dfrac{225}{4}=\dfrac{441}{4}+36\cdot2-21\cdot6\sqrt{2}\cos\beta\\\dfrac{225}{4}=\dfrac{441}{4}+72-126\sqrt{2}\cos\beta[/tex]

[tex]126\sqrt{2}\cos\beta=\dfrac{441}{4}+72-\dfrac{225}{4}\\126\sqrt{2}\cos\beta=\dfrac{216}{4}+72\\126\sqrt{2}\cos\beta=54+72\\126\sqrt{2}\cos\beta=126\quad|:126\\\sqrt{2}\cos\beta=1\quad|\cdot\sqrt{2}\\2\cos\beta=\sqrt{2}\quad|:2\\\cos\beta=\dfrac{\sqrt{2}}{2}[/tex]

Obliczenie odcinka x:

[tex]x^2=|DB|^2+|BC|^2-2|DB||BC|\cos\beta\\x^2=\left(\dfrac{15}{2}\right)^2+\left(6\sqrt{2}\right)^2-2\cdot\dfrac{15}{2}\cdot6\sqrt{2}\cdot\dfrac{\sqrt{2}}{2}\\x^2=\dfrac{225}{4}+36\cdot2-15\cdot3\sqrt{2}\cdot\sqrt{2}\\x^2=\dfrac{225}{4}+72-45\cdot2\\x^2=\dfrac{225}{4}+72-90\\x^2=\dfrac{225}{4}-18\\x^2=\dfrac{225}{4}-\dfrac{72}{4}\\x^2=\dfrac{153}{4}\\x=\dfrac{\sqrt{153}}{2}\\x=\dfrac{\sqrt{9\cdot17}}{2}\\x=\dfrac{3\sqrt{17}}{2}[/tex]

Obliczenie cosinusa kąta α:

[tex]|AC|^2=|AD|^2+x^2-2|AD|x\cos\alpha\\\left(\dfrac{15}{2}\right)^2=3^2+\left(\dfrac{3\sqrt{17}}{2}\right)^2-2\cdot3\cdot\dfrac{3\sqrt{17}}{2}\cos\alpha\\\dfrac{225}{4}=9+\dfrac{153}{4}-3\cdot3\sqrt{17}\cos\alpha\\\dfrac{225}{4}=\dfrac{36}{4}+\dfrac{153}{4}-9\sqrt{17}\cos\alpha[/tex]

[tex]9\sqrt{17}\cos\alpha=\dfrac{36}{4}+\dfrac{153}{4}-\dfrac{225}{4}\\9\sqrt{17}\cos\alpha=-\dfrac{36}{4}\\9\sqrt{17}\cos\alpha=-9\quad|:9\\\sqrt{17}\cos\alpha=-1\quad|\cdot\sqrt{17}\\17\cos\alpha=-\sqrt{17}\quad|:17\\\cos\alpha=-\dfrac{\sqrt{17}}{17}[/tex]

Obliczenie sinusa kąta α:

Uwaga: Kąt α jest kątem rozwartym, ponieważ cosinus α jest ujemny. Sinus kąta rozwartego jest dodatni.

Jedynka trygonometryczna:

[tex]\sin^2\alpha+\cos^2\alpha=1[/tex]

[tex]\sin^2\alpha+\left(-\dfrac{\sqrt{17}}{17}\right)^2=1\\\sin^2\alpha+\dfrac{17}{289}=1\\\sin^2\alpha+\dfrac{1}{17}=1\\\sin^2\alpha=1-\dfrac{1}{17}\\\sin^2\alpha=\dfrac{17}{17}-\dfrac{1}{17}\\\sin^2\alpha=\dfrac{16}{17}\\\sin\alpha=\dfrac{4}{\sqrt{17}}\\\sin\alpha=\dfrac{4\sqrt{17}}{17}[/tex]

Odpowiedź:

w Biblii mamy tylko kilka fragmentów o stroju Jana Chrzciciela. Jednak jego ubiór był tak specyficzny i skromny, że nie budził żadnych emocji. Możemy tylko napisać, że:

⦿ jego strój był wykonany z sierści wielbłądziej

⦿ na wysokości bioder, był opasany skórzanym pasem

⦿ żywił się szarańczą i miodem leśnym

Wyjaśnienie:

⦿ (Mt 3,4) "Sam zaś Jan nosił odzienie z sierści wielbłądziej i pas skórzany około bioder, a jego pokarmem była szarańcza i miód leśny."

⦿ (Mk 1, 6) "Jan nosił odzienie z sierści wielbłądziej i pas skórzany około bioder, a żywił się szarańczą i miodem leśnym."

____________________________________________

Jan Chrzciciel był synem Zachariasza i Elżbiety. Urodził się prawdopodobnie w tym samym okresie co Jezus, w mieście Judzie.  Po śmierci  rodziców wyruszył na pustynię i tam  nad rzeką Jordan chrzcił ludzi i przygotowywał ludzi na nadejście Mesjasza. Mówił sam o sobie "Jam głos wołającego na pustyni: Prostujcie drogę Pańską, jak powiedział prorok Izajasz" (J1, 23). Według Biblii, to on właśnie ochrzcił samego Jezusa. Jan Chrzciciel został ścięty w wyniku intrygi i kapryśności żony Heroda -Herodiady.

Zadanie polega na opisaniu Niepokalanego Poczęcia Najświętszej Maryi Panny.

Uroczystość Niepokalanego Poczęcia Najświętszej Maryi Panny jest obchodzona w kościele katolickim 8 grudnia. Przypomina ona o tym, że Maryja już od swego poczęcia była nienaznaczona grzechem pierworodnym, była czysta. Dogmat Niepokalanego Poczęcia został ogłoszony w 1854 r.

Maryja jest wolna od wszelakich grzechów, od samego początku swojego życia jej przeznaczeniem było urodzić Jezusowi Chrystusowi i tylko ona mogła tego dokonać. Bóg zdecydował o tym, że to właśnie ona da życie Synowi Bożemu i dlatego uwolnił jej duszę od grzechu.

#SPJ3