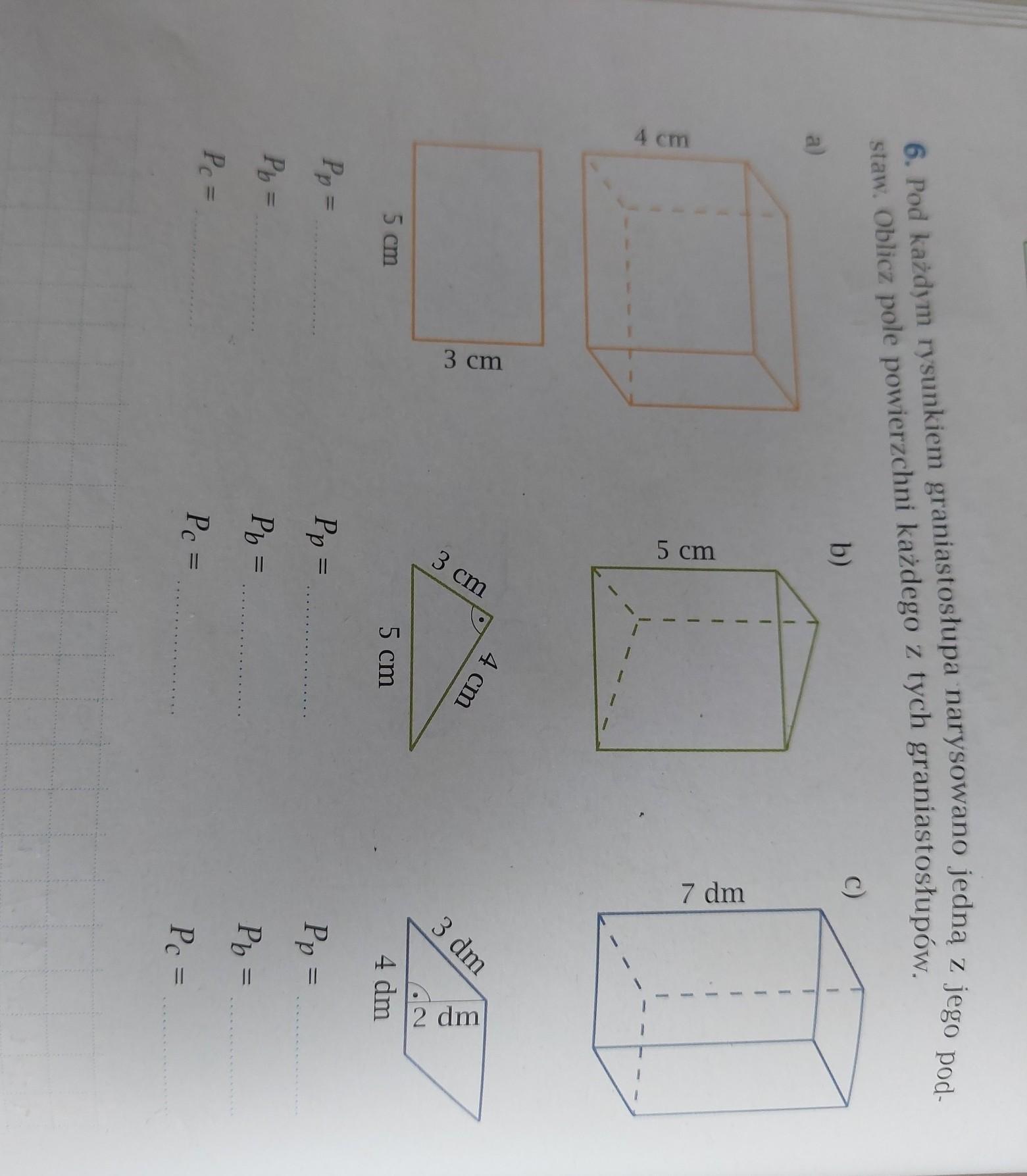
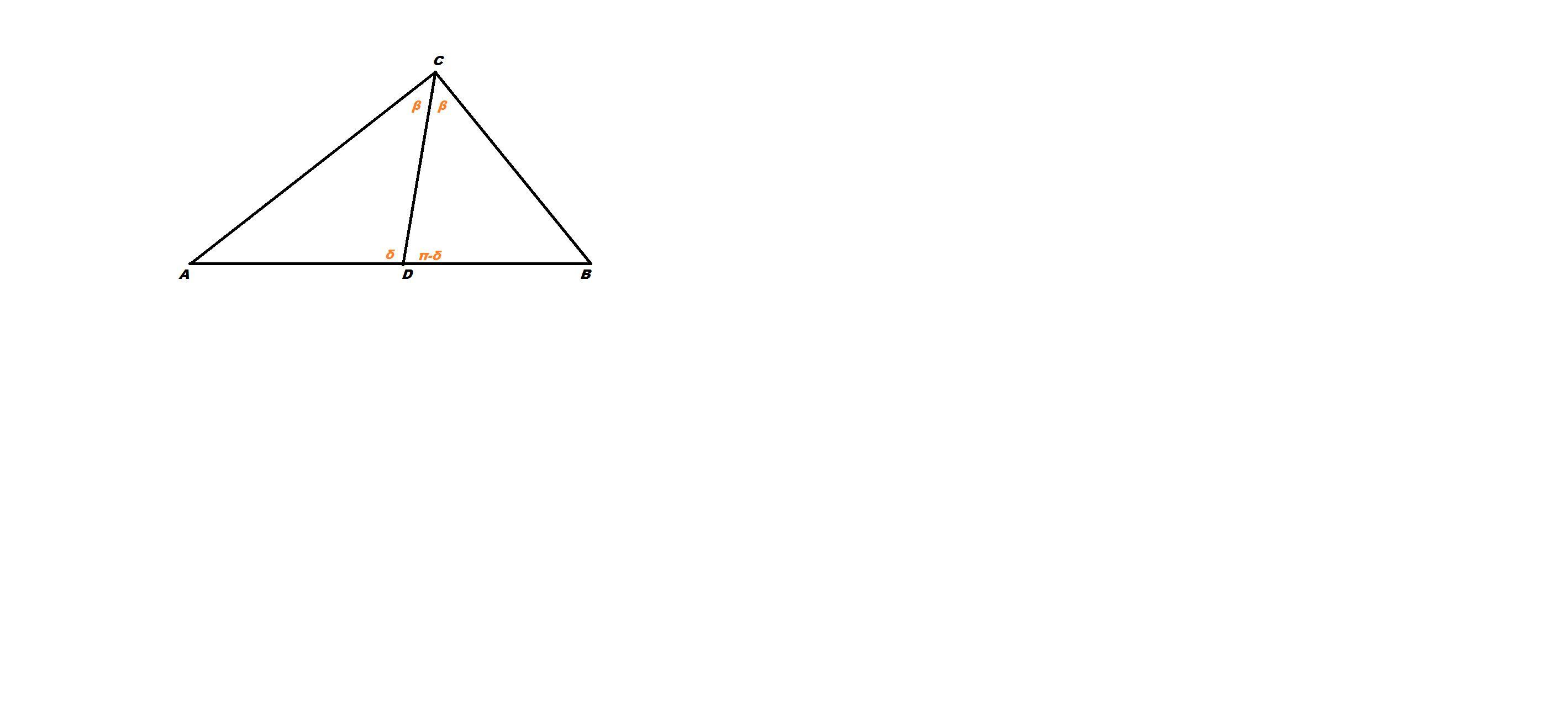Zadanie w załączniku. Wszelkie informacje w komentarzu pod zadaniem.

-
Temat:
Język niemiecki -
Autor:
halfmast -
Utworzono:
1 rok temu
Odpowiedzi 1
7-Was hast du gestern in deinem Zimmer gemacht?-Ich habe ein Buch gelesen und meine Hausaufgaben gemacht.
-Wo hast du am Morgen gefrühstückt?- Ich habe in der Küche gefrühstückt.
-Wie lange hast du vorgestern ferngesehen?-Ich habe vorgestern leider nicht ferngesehen.
-
Autor:
french fryu88q
-
Oceń odpowiedź:
19
Znasz odpowiedź? Dodaj ją tutaj!
Wybierz język i region
How much to ban the user?
1 hour
1 day
100 years