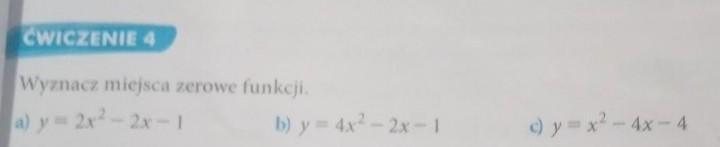Proszę o szybką pomoc!!!!

5.

[tex]a) \ 2^{4}-3^{2} = 2\times2\times2\times2 - 3\times3 = 16-9 = 7\\\\b) \ 5^{2}-4^{2} = 25-16 = 9[/tex]

Odpowiedź:

Szczegółowe wyjaśnienie:

Jeżeli wielkości x i y są odwrotnie proporcjonalne, to ich iloczyn jest stały:

Wzór proporcjonalności odwrotnej:

Obliczamy współczynnik proporcjonalności a = x · y

a = 1/2 · 1/3

Podstawiamy:

b) P(√2, √3)

Obliczamy współczynnik proporcjonalności a = x · y

a = √2 · √3

Podstawiamy:

Odpowiedź:

Szczegółowe wyjaśnienie:

Miejsce zerowe funkcji, jest to taki argument (x), dla którego wartość funkcji (y) wynosi 0.

W interpretacji geometrycznej, jest to miejsce przecięcia wykresu funkcji z osią OX.

W każdym z przykładów mamy do rozwiązania równanie y = 0.

Mając równanie kwadratowe postaci ax² + bx + c = 0.

Liczba rozwiązań takiego równania jest zależna od wartości wyróżnika trójmianu kwadratowego Δ = b² - 4ac.

Jeżeli Δ < 0, to równanie nie posiada rozwiązań w zbiorze liczb rzeczywistych (funkcja nie ma miejsc zerowych).

Jeżeli Δ = 0, t równanie ma jedno rozwiązanie w zbiorze liczb rzeczywistych (funkcja posiada jedno miejsce zerowe) postaci

Jeżeli Δ > 0, to równanie posiada dwa różne rozwiązania w zbiorze liczb rzeczywistych (funkcja posiada dwa miejsca zerowe) postaci

2x² - 2x - 1 = 0

a = 2, b = -2, c = -1

Δ = (-2)² - 4 · 2 · (-1) = 4 + 8

√Δ = √12 = √(4 · 3) = 2√3

x₁ = (-(-2) - 2√3)/(2 · 2)

x₁ = (2 - 2√3)/4   /skracamy przez 2

x₂ = (-(-2) + 2√3)/(2 · 2)

x₂ = (2 + 2√3)/4   /skracamy przez 2

4x² - 2x - 1 = 0

a = 4, b = -2, c = -1

Δ = (-2)² - 4 · 4 · (-1) = 4 + 16

√Δ = √20 = √(4 · 5) = 2√5

x₁ = (-(-2) - 2√5)/(2 · 4)

x₁ = (2 - 2√5)/8    /skracamy przez 2

x₂ = (-(-2) + 2√5)/(2 · 4)

x₂ = (2 + 2√5)/8    /skracamy przez 2

x² - 4x - 4 = 0

a = 1, b = -4, c = -4

Δ = (-4)² - 4 · 1 · (-4) = 16 + 16

√Δ = √32 = √(16 · 2) = 4√2

x₁ = (-(-4) - 4√2)/(2 ·1)

x₁ = (4 - 4√2)/2   /skracamy przez 2

x₂ = (-(-4) + 4√2)/(2 · 1)

x₂ = (4 + 4√5)/2    /skracamy przez 2