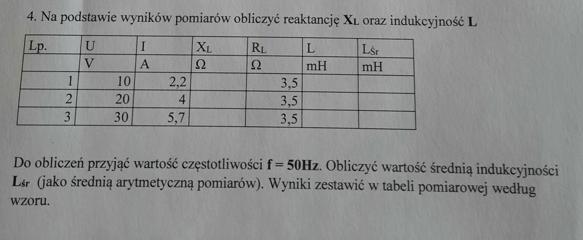
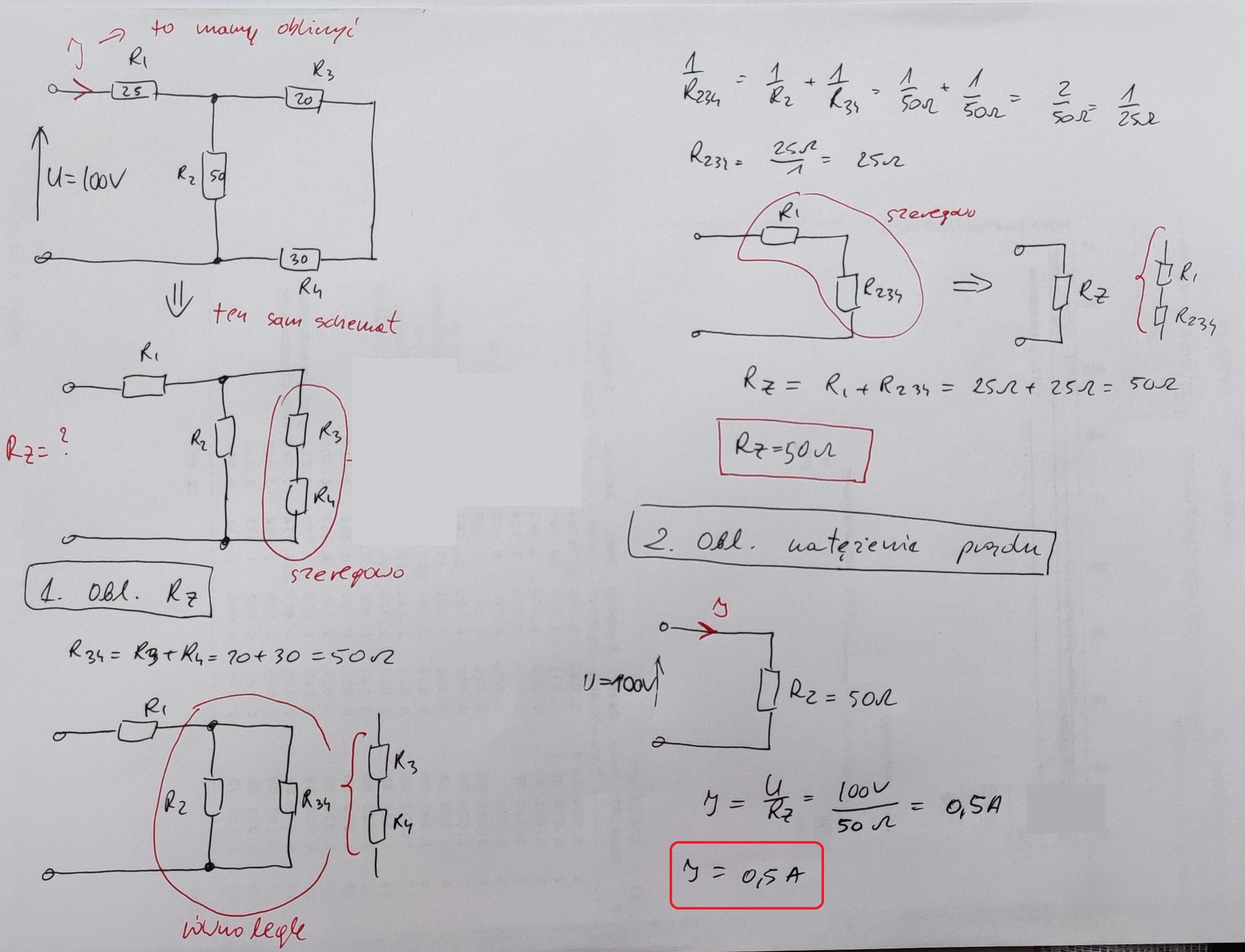
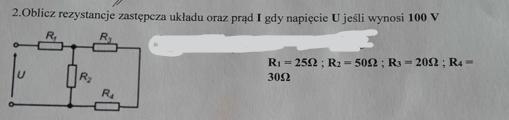daje naj utwórz czas przeszły perfekt. 1. Du malst ein Bild. Du hast ein Bild ............... 2. Wir raumen das zimmer auf. Wir ................ meine arbeit ........... 3. Ich prasentiere meine Arbeit. Ich .............. meine Arbeit ..................... 4. Ihr lest ein Buch. Ihr ............... ein Buch ................. 5. Er fahrt zur Arbeit Er ................. zur Arbeit ............ 6. Hast du heute noch nichts ................... ? (essen) + polskie tłumaczenie .......................................................................................... 7. Napisz, że wypiłeś wode mineralną.

1. 1 l = 1 dm3, d = 4dm, H = 10dm, r = 4/2 = 2cm

V = πr^2 * H = 3,14 * 2 * 2 * 10 = 125,6dm3 = 125,6 l

2. r = 3cm, H = 5 * 3cm = 15cm

P = 2Pp + Pb = 2πr^2 + 2πrH = 2πr(r + H) = 2 * 3,14 * 3 * (3 + 15) = 339,12 dm2

3. Przypadek 1: πd = 20cm <=> d = 20/3,14 = 6,37cm

Przypadek 2: πd = 30cm <=> d = 30/3,14 = 9,55cm

Szczegółowe wyjaśnienie:

Zadanie1.

[tex]d=4dm[/tex]   to  [tex]r=\frac{1}{2} d=2dm[/tex]

[tex]H=10dm[/tex]

[tex]\pi =3,14[/tex]

"Ile benzyny zmieści się w beczce" - należy więc obliczyć objętość beczki.

Korzystamy ze wzoru na objętość walca:  [tex]V=\pi r^{2} *H[/tex]

[tex]V=\pi *2^{2} *10=\pi *4*10=40\pi[/tex]

[tex]\pi =3,14[/tex]

[tex]V=40*3,14=125,6[/tex]

[tex]V=125,6[/tex] [tex]dm^{3}[/tex]  [tex]= 125,6[/tex] [tex]l[/tex]                     [tex]1litr=1dm^{3}[/tex]

W beczce zmieści się 125,6 litrów benzyny

Zadanie2.

[tex]r=3m[/tex]    [tex]H=5*3=15cm[/tex]

[tex]Pc =2*\pi r^{2} +2\pi rH[/tex]     ← wzór na pole powierzchni walca

[tex]Pc=2*\pi *3^{2} +2*\pi *3*15\\Pc=18\pi +90\pi \\Pc=108\pi[/tex]

Pole powierzchni walca wynosi 108π cm².

Zadanie 3

wymiary arkusza papieru: [tex]20cmx30cm[/tex]

Jeden bok arkusza będzie wysokością, a drugi obwodem koła o promieniu r, czyli obwodem podstawy walca o promieniu r.

rozważamy dwa przypadki

I.

H= 30cm, drugi bok to obwód podstawy walca: [tex]2\pi r=20cm[/tex]

[tex]2\pi r=20/:2\pi \\r=\frac{20\ }{2\pi } =\frac{10}{\pi }[/tex]

Przyjmujemy: [tex]\pi =3,14[/tex]

[tex]r=\frac{10}{3,14}[/tex]

r ≈ 3,185 cm                  d-średnica koła ( średnica walca)

to    d=2·r = 2·3,185 cm ≈ 6,37 cm

Średnica walca wynosi 6,37 cm.

II.

H= 20cm ,drugi bok to obwód podstawy walca: [tex]2\pi r=30cm[/tex]

[tex]2\pi r=30 /:2\pi[/tex]

[tex]r=\frac{30}{2\pi } =\frac{15}{\pi }[/tex]

Przyjmujemy: [tex]\pi =3,14[/tex]

[tex]r=\frac{15}{3,14}[/tex]

r ≈ 4,777 cm

d= 2r = 2· 4,777 ≈ 9,55 cm

Średnica walca w tym przypadku wynosi 9,55 cm.

Odp. Walec może mieć średnicę długości 6,37 cm lub 9,55 cm.

Strona bierna na ogół jest prosta.Każdy czas na swoją wersję - załapać jest dosyć prosto:Weźmy na warsztat zdanie w Present Simple:He writes a book. (On napisał książkę) Zadaj sobie pytanie: Jak byś to przekształcił na polską stronę bierną? Książka jest pisana przez niego (ważna jest zgodność czasowa, żeby się nie pokićkało w praniu!)czyli ze zdania wyjściowego robimy:A book is written by him. -> zamieniliśmy kolejnością rzeczowniki, i teraz książka jest podmiotem, nie "on". Dodatkowo, słówko "by" jest mega ważne - znaczy po prostu "przez". (nie jest wymagane, ale fajnie by było, żeby się pojawiło.)To samo zdanie w innych czasach weźmy:Past Simple: He wrote a book -> A book was written by him.Present Perfect: He has written a book. -> a book has been written by him.Future Simple: He will write a book. -> a book will be written by him.co możemy zauważyć? a no, że w każdym zdaniu czasownik zmienił formę na 3 formę czasownika z tabeli. I tak jest zawsze. Co jeszcze? jeżeli w zdaniu "elementów czasownikowych miałeś/aś 1, to w stronie biernej będzie o jeden więcej.Past Simple - elementem czasownikowym jest tylko "wrote", dlatego w stronie biernej będzie "was written" -> +1 element czasownikowyPresent Perfect - "has written" -> +1 element, więc będzie has been written.Ale, jaka jest zasada? Tutaj króluje czasownik "be" w odpowiednim czasie i formie, tzn. wzór masz taki:nowy podmiot + be+ czasownik z 3 tabeli w kolumnie.To weźmy na warsztat przyklady:She didn't take my wallet - jaki to czas? past simple. Co będzie nowym podmiotem? "my wallet" (przetłumacz sobie zdanie na polski i z niego utwórz po polsku stronę bierną.) Okej, forma przeszła od czasownika "be"? Was/were (w zależności od liczby podmiotu.) no i potem dodajemy czasownik w 3-ciej formie. Widzimy, że chodzi tu o przeczenie, w którym miejscu możemy dodać "not" (formę przeczącą)? no tylko i wyłącznie do "be"She didn't take my wallet - My wallet WASN'T taken. (by her)They will send the letters - analogicznie: przetłumacz, jaki to czas? ile jest elementów czasownikowych? co będzie nowym podmiotem? Okej, to jest future simple - mamy "willa" którego nie można usunąć. Jeżeli w jakimkolwiek zdaniu twierdzącym wystąpi operator, to znaczy że musi tam być i tyle. Dlatego też i w stronie biernej musi się pojawić.They will send the letters - the letters will be sent (by them). - okej, dlaczego po willu jest samo "be"? bez żadnej zmienionej formy? a no, zasada jest taka, którą trzeba sobie wbić do głowy, że jak mamy will, to po nim jest zawsze, ale to zawsze bezokolicznik.Okej, to reszta przykładów.3. The cookies haven't been baked by him. ("he" to była liczba pojedyncza, dlatego było "has". Nowy podmiot zmienia formę na "have")4. Skirts aren't ironed by her. -> w present simple/continous czasownik "be" przybiera formę teraźniejszą (am/is/are)5.  Our key has been lost by us.6. the shop was opened by them.7. the bathroom is cleaned by him.8. the songs won't be downloaded by them.9. vegetables aren't eaten by me.10. flowers aren't watered by us.Mam nadzieję, że pomogłam, w razie pytań proszę o komentarz.

Odpowiedź:

Wyjaśnienie:

Odpowiedź:

Zrób plakat z dzieckiem z sercem narysowanym(w sensie że "❤️") po czym obok narysuj uśmiechnięta starszą panią w kościele modlącą się