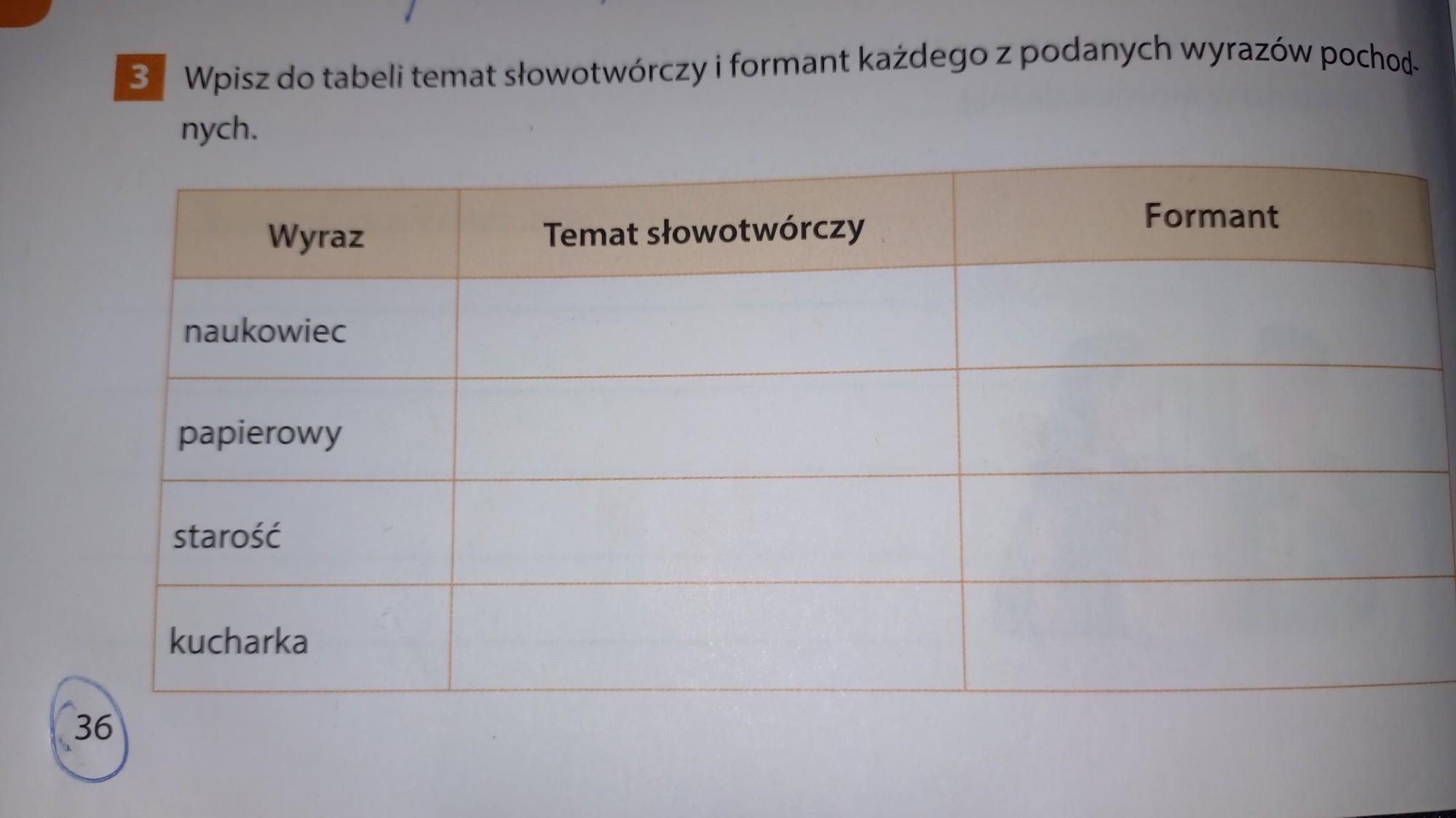
zakrles nazwy czesci garderoby znajdujace sie na zdjeciu a nastepnie podkresl w podanych wyrazeniach koncowki przykiotnikow. POTRZEBUJE NA JUZ!!

-
Temat:
Język niemiecki -
Autor:
melvin -
Utworzono:
1 rok temu
Odpowiedzi 1
Odpowiedź:
Mam nadzieję, że pomogłam :)

-
Autor:
scott677
-
Oceń odpowiedź:
8
Znasz odpowiedź? Dodaj ją tutaj!
Wybierz język i region
How much to ban the user?
1 hour
1 day
100 years