Dokończ zdania po Rosyjsku1. Во время летнок каникул я буду....2. Я буду по - сещать...3. Мы будем жить...4. Они поедут...5. А кто будет отдыхать...Pls help na jutro mam to zrobić​

Twierdzenie o dwusiecznej kąta wewnętrznego w trójkącie

Dwusieczna kąta wewnętrznego w trójkącie dzieli przeciwległy bok proporcjonalnie do długości pozostałych boków.

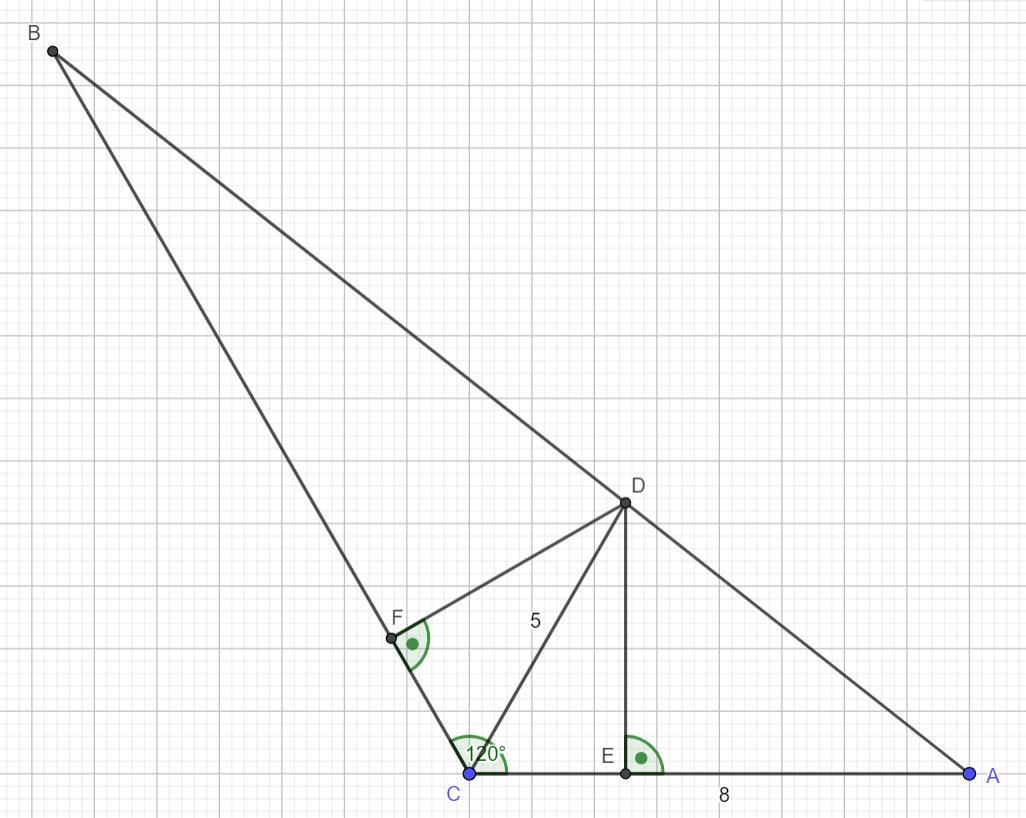
W oznaczeniach przyjętych na rysunku w załączniku treść twierdzenia wyraża proporcja:

[tex]\dfrac{|AD|}{|BD|}=\dfrac{|AC|}{|BC|}[/tex]

Obliczenie długości boków CE i DE (trójkąt 30°, 60°, 90°) oraz CF i DF:

[tex]|CE|=\dfrac{1}{2}|CD|=\dfrac{1}{2}\cdot5=\dfrac{5}{2}\\|CF|=|CE|=\dfrac{5}{2}[/tex]

[tex]|DE|=|CE|\sqrt{3}=\dfrac{5}{2}\sqrt{3}\\|DF|=|DE|=\dfrac{5}{2}\sqrt{3}[/tex]

Obliczenie długości boków AE i AD:

[tex]|AE|=|AC|-|CE|=8-\dfrac{5}{2}=8-2\dfrac{1}{2}=5\dfrac{1}{2}=\dfrac{11}{2}[/tex]

[tex]|AD|^2=|AE|^2+|DE|^2\\|AD|^2=\left(\dfrac{11}{2}\right)^2+\left(\dfrac{5}{2}\sqrt{3}\right)^2\\|AD|^2=\dfrac{121}{4}+\dfrac{25}{4}\cdot3\\|AD|^2=\dfrac{121}{4}+\dfrac{75}{4}\\|AD|^2=\dfrac{196}{4}\\|AD|=\dfrac{14}{2}\\|AD|=7[/tex]

Wyznaczenie długości BD z twierdzenia o dwusiecznej:

[tex]\dfrac{7}{|BD|}=\dfrac{8}{|BC|}[/tex]

[tex]8|BD|=7|BC|\quad|:8\\|BD|=\dfrac{7}{8}|BC|[/tex]

Obliczenie długości odcinka BC:

[tex]|BF|=|BC|-|CF|=|BC|-\dfrac{5}{2}\\|BF|^2+|DF|^2=|BD|^2\\\left(|BC|-\dfrac{5}{2}\right)^2+\left(\dfrac{5}{2}\sqrt{3}\right)^2=\left(\dfrac{7}{8}|BC|\right)^2\\|BC|^2-5|BC|+\dfrac{25}{4}+\dfrac{75}{4}=\dfrac{49}{64}|BC|^2\\|BC|^2-5|BC|+\dfrac{100}{4}=\dfrac{49}{64}|BC|^2\\|BC|^2-5|BC|+25-\dfrac{49}{64}|BC|^2=0\\\dfrac{15}{64}|BC|^2-5|BC|+25=0\quad|:5\\\dfrac{3}{64}|BC|^2-|BC|+5=0\quad|\cdot64\\3|BC|^2-64|BC|+320=0[/tex]

[tex]\Delta=(-64)^2-4\cdot3\cdot320=4096-3840=256\\\sqrt{\Delta}=16[/tex]

[tex]|BC|_1=\dfrac{64-16}{2\cdot3}=\dfrac{48}{6}=8=|AC|[/tex]

[tex]|BC|_2=\dfrac{64+16}{2\cdot3}=\dfrac{80}{6}=13\dfrac{2}{6}=13\dfrac{1}{3}=|BC|[/tex]

Odpowiedź: Odcinek BC ma długość [tex]13\frac{1}{3}[/tex] cm.

Pole trójkąta ADC:

[tex]P=\dfrac{|AC|\cdot|DE|}{2}=\dfrac{8\cdot\dfrac{5}{2}\sqrt{3}}{2}=8\cdot\dfrac{5}{2}\sqrt{3}\cdot\dfrac{1}{2}=10\sqrt{3}\mbox{ cm}^2[/tex]

Pole trójkąta DBC:

[tex]P=\dfrac{|BC|\cdot|DF|}{2}=\dfrac{13\dfrac{1}{3}\cdot\dfrac{5}{2}\sqrt{3}}{2}=\dfrac{40}{3}\cdot\dfrac{5}{2}\sqrt{3}\cdot\dfrac{1}{2}=\dfrac{50}{3}\sqrt{3}\mbox{ cm}^2[/tex]

1. KOH+HNO2--->KNO2+H2O

2 K+2 HNO2--->2 KNO2+H2

K2O+2 HNO2--->2 KNO2+H2O

K2O+N2O3--->2 KNO2

2 KOH+N2O3--->2 KNO2+H2O

2. Ca(OH)2+H2SO4--->CaSO4+2 H2O

Ca+H2SO4--->CaSO4+H2

CaO+H2SO4--->CaSO4+H2O

CaO+SO3--->CaSO4

Ca(OH)2+SO3--->CaSO4+H2O

3. Al(OH)3+H3PO4--->AlPO4+3 H2O

2 Al+2 H3PO4--->2 AlPO4+3 H2

Al2O3+2 H3PO4--->2 AlPO4+3 H2O

2 Al2O3+P4O10--->4 AlPO4

4 Al(OH)3+P4O10--->4 AlPO4+6 H2O

4. NaOH+HCl--->NaCl+H2O

2 Na+Cl2--->2 NaCl

2 Na+2 HCl--->2 NaCl

Na2O+HCl--->2 NaCl+H2O

Na3PO4+AlCl3--->3 NaCl+AlPO4↓

Odpowiedź:

1. I've got

2.I haven't got

3.I haven't got

4.I have

5. I have