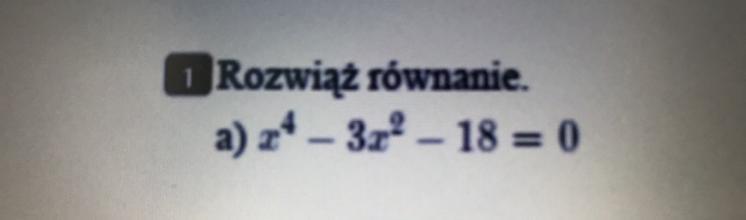Proszę o rozwiązanie
-
Temat:
Matematyka -
Autor:
rhett13 -
Utworzono:
1 rok temu
Odpowiedzi 1
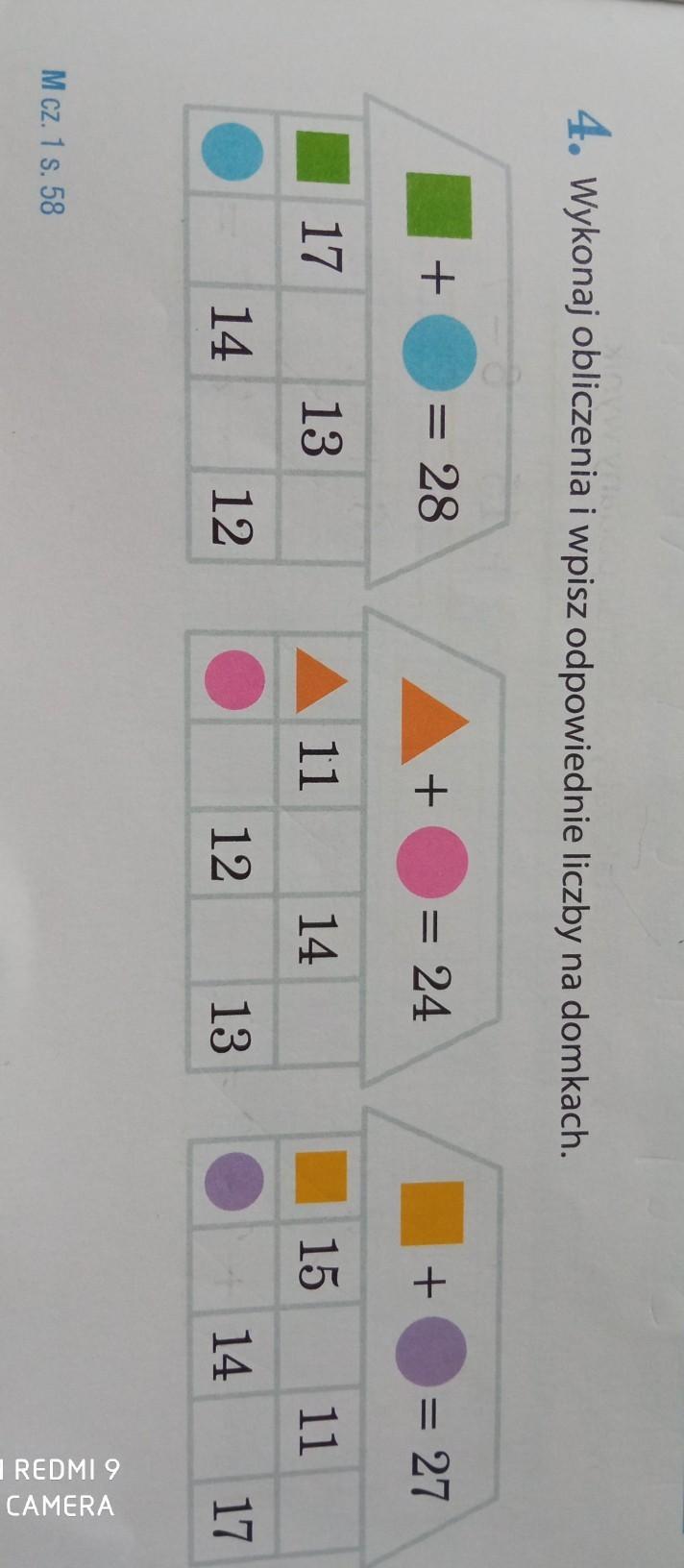
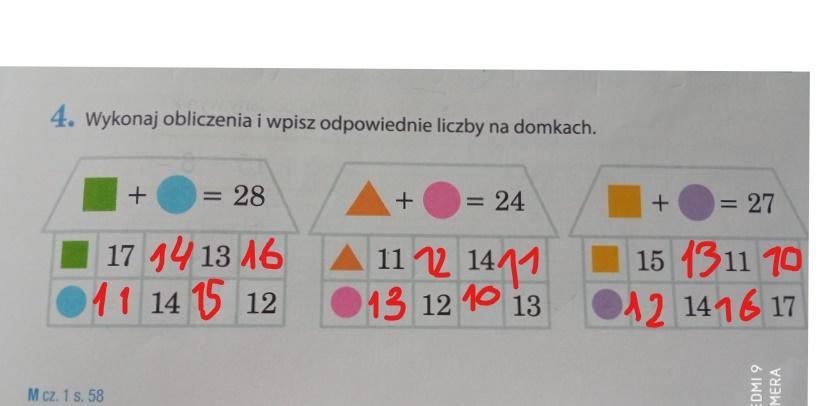
mam nadzieję ,że pomogłam:)
-
Autor:
javier2zn9
-
Oceń odpowiedź:
13
Znasz odpowiedź? Dodaj ją tutaj!
Wybierz język i region
How much to ban the user?
1 hour
1 day
100 years