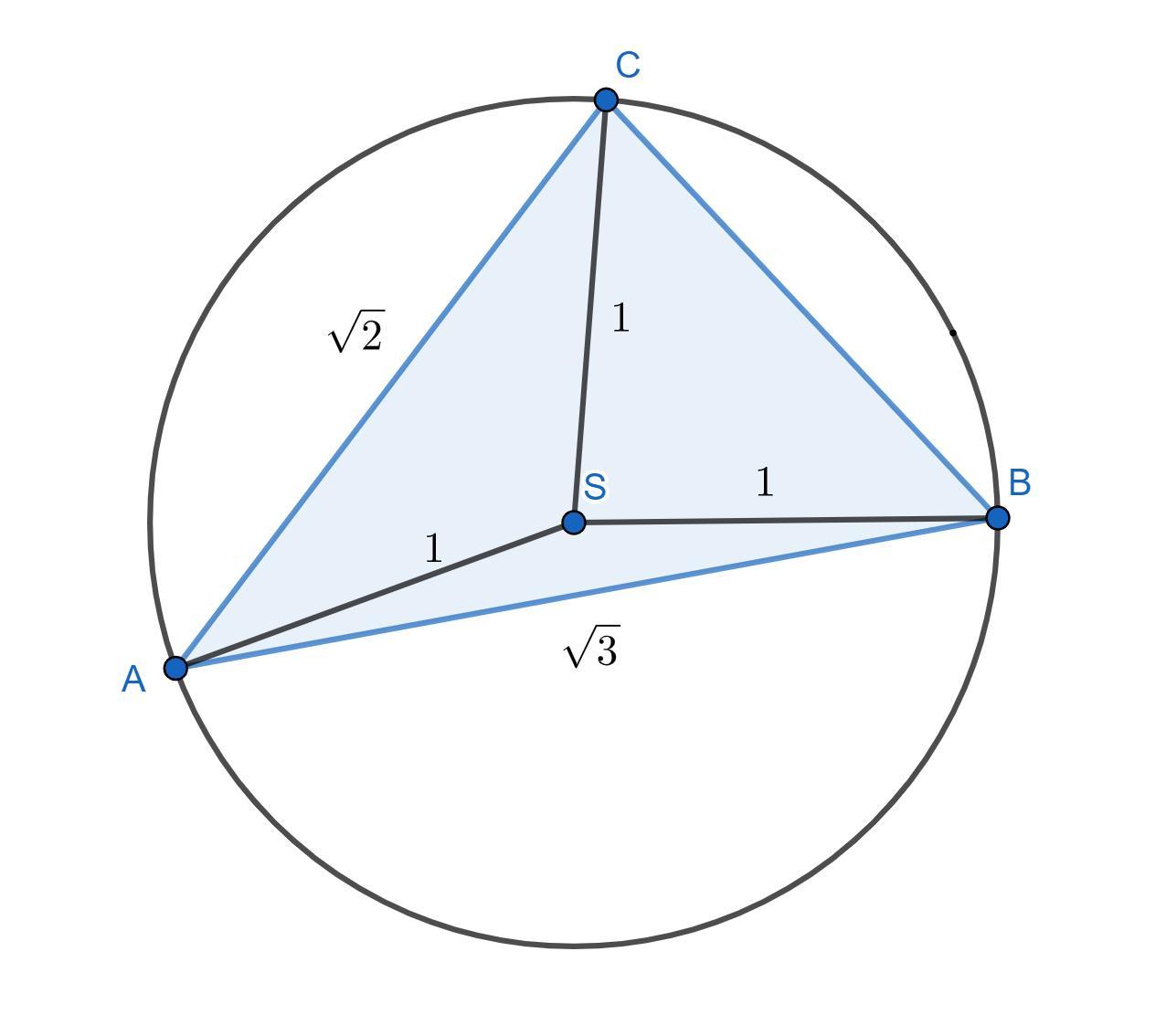
Trójkąt ABC jest wpisany w okrąg o promieniu 1, przy czym |AB| = √3 i |AC| = √2. Rozwiąż trójkąt ABC. PLIS POMOZCIE DAM NAJJJ

Odpowiedzi 1

Twierdzenie sinusów.

  1. Zaczynamy od rysunku (poniżej).
  2. Z twierdzenia sinusów dla trójkąta wiemy, że:[tex]\frac{a}{\sin |\angle A|} = \frac{b}{\sin |\angle B|} =\frac{c}{\sin |\angle C|} = 2R[/tex]gdzie kąt [tex]\angle X[/tex] znajduje się "na przeciwko" boku [tex]x[/tex], zaś [tex]R[/tex] to promień okręgu opisanego.
  3. Z danych z zadania mamy:[tex]\frac{\sqrt3}{\sin |\angle C|} = 2\cdot 1\\ \sin |\angle C| = \sqrt 3 /2[/tex]czyli [tex]|\angle C| = 60^\circ[/tex]oraz[tex]\frac{\sqrt2}{\sin |\angle B|} = 2\cdot 1\\ \sin |\angle B| = \sqrt 2 /2[/tex]czyli [tex]|\angle B| = 45^\circ[/tex]
  4. Stąd, wiedząc, że suma kątów w trójkącie to [tex]180^\circ[/tex]:[tex]| \angle A | = 180^\circ - 60^\circ - 45 ^\circ = 75^\circ[/tex]
  5. Zaś stąd (znów z tw. sinusów):[tex]|BC| = 2 \cdot \sin 75 ^\circ = \frac{1+\sqrt3}{\sqrt 2}[/tex]

Warto przy okazji pamiętać o "pokrewnym" twierdzeniu cosinusów:[tex]c^2 = a^2 + b^2 - 2ab \cos |\angle (a,b)|[/tex]

answer img

Znasz odpowiedź? Dodaj ją tutaj!

Can't find the answer?

Other related questions that may help you

Dokoncz opowiadanie. Na podstawie ilustracji i wlasnych pomyslow dopisz jego rozwiniecie i zakonczenie. (w miare krótkie) Dziekuje daje naj naj
question img

wręczając mamaie kwiaty, mama spytała się skąd je zerwała Asia powiedziała ze znalazłam je w lesie. mam powiedziała córce że nie można zrywać kwiatów które są pod ochroną

karta pracy pan tadeusz księga 6 zaścianek​
question img

Wygląd Dobrzynia

Dom Dobrzyńskich stał między karczmą, a kościołem. Był zaniedbany. Ogród nie miał płotu, brama była popsuta i nikt nie dbał o jego otoczenie. Posiadał wozownie, oborę, świetlicę i stajnię. Jak określił go sam autor: dwór przypominał królikarnię.

Szlachta Dobrzyńska

Szlachcice byli mężni, a szlachcianki niezwykle piękne. Kiedyś byli dobrze usytuowaną szlachtą goszczącą na sejmikach i walczącą w królewskim wojsku. Ostatnimi czasy jednak zubożeli i pracować musieli sami na siebie jako chłopstwo. Mieli czarne włosy i oczy. Charakteryzowały ich wysokie czoła i orle nosy. Zachowali mazurską mowę i zwyczaje.

Maciej Dobrzyński

Stał na czele rodziny. Nazywany był Kurkiem na kościele, Zabokiem, Królikiem i Maćkiem nad Maćkami. Miał 72 lata. Był niski, ale dziarski. Był bystry, sprytny, odważny i łatwo popadał w gniew.

Co mówi sędzia na temat planów Jacka Soplicy wobec Tadeusza i Zosi?

Mówi, że to nie jego sprawa i, że zajmowanie się nią go nudzi. Na koniec pomaga jednak Jackowi namówić Tadeusza na ten związek.

Czyje przybycie zapowiada Robak? Do czego namawia sędziego?

Zapowiada przybycie Napoleona. Namawia go do walki o Polskę.

Pan Tadeusz to napisana przez Adama Mickiewicza dwutomowa epopeja narodowa. Na kartach dwunastu ksiąg, pisanych wierszem opisane zostały szlacheckie historie rodu Sopliców.

Na mapie oznaczono wybrane miasta Stanów Zjednoczonych. Literami A i B oznaczonodwie wybrane technopolie. Barwami przedstawiono strefy czasowe kontynentalnej częściStanów Zjednoczonych.Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, albo F - jeślijest fałszywe.Technopolie to miejsca koncentracji przemysłu ściśle współpracującegoz uniwersytetami i instytutami naukowymi.-Na mapie literą B oznaczono technopolię – Dolinę Krzemową.​
question img

Odpowiedź:

1 P

2 F

Wyjaśnienie:

powinno być dobrze bo na lekcji robiłam

Światło zielone ma w powietrzu długość fali równą 520nm. Długosć tej fali w wodzie jest równa? ( prędkosć swiatła w powietrzu 3 * 10 ^ 8 * m/s)​

Fale świetlne

λ₂ ≈ 391 nm = 0,000000391 m

Dane:

λ₁ = 520 nm = 0,00000052 m

v₁ = 300000000 m/s

Szukane:

λ₂ = ?

Rozwiązanie:Z prawa Snelliusa wynika, że stosunek prędkości w ośrodkach jest odwrotnie proporcjonalna do stosunku współczynników załamania światła w danych ośrodkach:

 [tex]\frac{v_1}{v_2} = \frac{n_2}{n_1}[/tex]

Współczynnik załamania światła w powietrzu jest w przybliżeniu równy 1, a w wodzie 1,33, więc:

[tex]v_2 = \frac{v_1n_1}{n_2}[/tex]

Częstotliwość fali jest stała nie zależnie od ośrodka, w jakim się rozchodzi (o ile się w nim może rozchodzić). Częstotliwość fali światła zielonego jest równa:

 [tex]f = \frac{ \lambda_1}{v_1} = \frac{\lambda_2}{v_2}[/tex]

Więc prędkość fali światła zielonego w wodzie jest równa:

 [tex]\lambda_2 = \frac{v_2 \lambda_1}{v_1} = \frac{n_1v_1\lambda_1}{v_1n_2} = \frac{n_1\lambda_1}{n_2} = 390,9774... nm[/tex]

Other Matematyka Questions

Zaloguj się z Google

 lub

Zapomniałeś(aś) hasła?

Nie mam jeszcze konta, ale chcę je założyć Zarejestruj się

Wybierz język i region

English

United States

Polski

Polska

Português

Brasil

English

India

English

Philippines

Español

España

Bahasa Indonesia

Indonesia

Türkçe

Türkiye
How much to ban the user?
1 hour 1 day 100 years