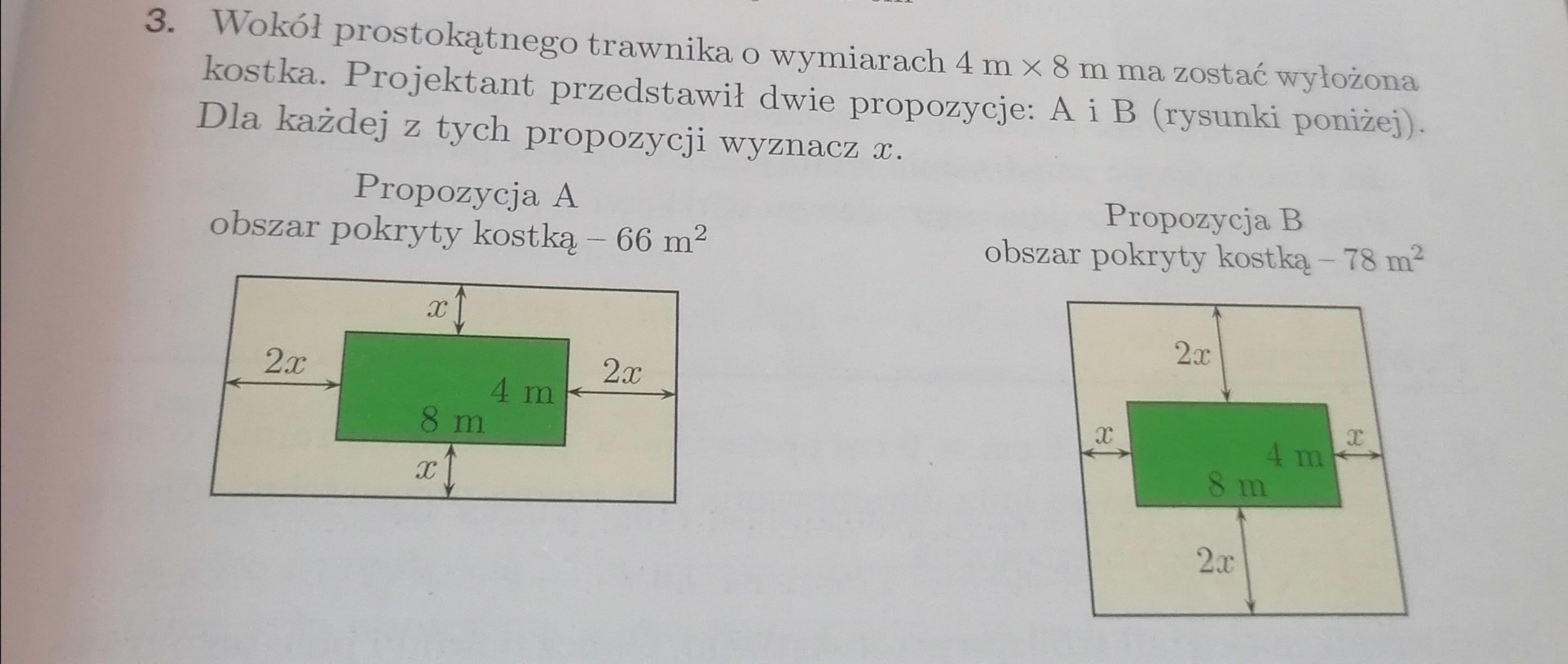
Propozycja BBłagam na teraz, daje naj i 60 pkt!

Temat:
Matematyka
Autor:
stephen
Utworzono:
1 rok temu

Odpowiedzi 2

Odpowiedź:

( 2x + 4 + 2 x)*( x + 8 + x) - 8*4 = 78

( 4x + 4)*( 2 x + 8) - 32 = 78

4*(x + 1)*2*(x + 4) = 110

8*( x² + 4 x + x + 4) = 110

8 x² + 40 x + 32 - 110 = 0

8 x² + 40 x - 78 = 0 / : 2

4 x² + 20 x - 39 = 0

Δ = 20² - 4*4*(-39) = 400 + 624 = 1024

√Δ = 32

x = [tex]\frac{- 20 +32}{8} = 1,5[/tex]

x = 1,5 m

=======

Szczegółowe wyjaśnienie:

Autor:

haydenn41f
Oceń odpowiedź:
15

Odpowiedź:

Propozycja A

x = 1,5 m

Propozycja B

x = 1,5 m

Szczegółowe wyjaśnienie:

Propozycja A

Pole powierzchni całego prostokąta (trawnik + kostka):

- długość [m]: 2x + 8 + 2x = 4x + 8 = 4(x + 2)

- szerokość [m]: x + 4 + x = 2x + 4 = 2(x + 2)

Pole, długość razy szerokość, [m²]:

4(x + 2)•2(x + 2) = 8(x + 2)² = 8(x² + 4x + 4) = 8x² + 32x + 32

Pole trawnika: 8•4 = 32 m²

Pole powierzchni kostki 66 m²

(pole całego prostokąta minus pole trawnika):

(8x² + 32x + 32) - 32 = 8x² + 32x = 66 /:2 to 4x² + 16x - 33 = 0

Należy rozwiązać ostatnie równanie:

ax² + bx + c = 0, wyróżnik równania Δ = b² - 4ac = 16² - 4•4•(-33) =

= 256 + 528 = 784 to √∆ = 28, to x1 = (- b - √∆)/2a < 0,

odpada, ponieważ długość |x| nie może być tylko ujemna;

x2 = x = (- b + √∆)/2a = (- 16 + 28)/2•4 = 12/8 = 3/2 = 1,5 m

to: Odpowiedź: x = 3/2 = 1,5 m

Propozycja B

Pole powierzchni całego prostokąta (trawnik + kostka):

- długość [m]: x + 8 + x = 2x + 8 = 2(x + 4)

- szerokość [m]: 2x + 4 + 2x = 4x + 4 = 4(x + 1)

Pole, długość razy szerokość, [m²]:

2(x + 4)•4(x + 1) = 8(x² + 4x + x + 4) = 8(x² + 5x + 4) = 8x² + 40x + 32

Pole trawnika: 8•4 = 32 m²

Pole powierzchni kostki 78 m²

(pole całego prostokąta minus pole trawnika):

(8x² + 40x + 32) - 32 = 8x² + 40x = 78 /:2 to 4x² + 20x - 39 = 0

Należy rozwiązać ostatnie równanie:

ax² + bx + c = 0, wyróżnik równania Δ = b² - 4ac = 20² - 4•4•(-39) =

= 400 + 624 = 1024 to √∆ = 32, to x1 = (- b - √∆)/2a < 0,

odpada, ponieważ długość |x| nie może być ujemna;

x2 = x = (- b + √∆)/2a = (- 20 + 32)/2•4 = 12/8 = 3/2 = 1,5 m

to: Odpowiedź: x = 3/2 = 1,5 m

Autor:

elfs1rf
Oceń odpowiedź:
9

Propozycja BBłagam na teraz, daje naj i 60 pkt!

Odpowiedzi 2

Znasz odpowiedź? Dodaj ją tutaj!

Can't find the answer?

Other Matematyka Questions

Propozycja BBłagam na teraz, daje naj i 60 pkt! ​

Odpowiedzi 2

Znasz odpowiedź? Dodaj ją tutaj!

Can't find the answer?

Other related questions that may help you

Other Matematyka Questions

Propozycja BBłagam na teraz, daje naj i 60 pkt!