Oblicz wartość wyrażenia 2x - 8 dla x - 3

Odpowiedź:

[tex]P_\triangle=24[/tex]

Szczegółowe wyjaśnienie:

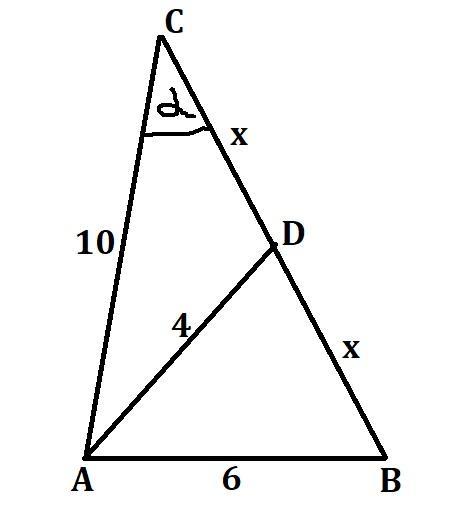
Skorzystamy dwukrotnie z tw. cosinusów w trójkątach ABC i ADC.

[tex]\left \{ {{6^2=10^2+(2x)^2-2*10*2x*\cos\alpha} \atop {4^2=10^2+x^2-2*10*x*\cos\alpha}} \right. \\\left \{ {{36=100+4x^2-40x\cos\alpha} \atop {16=100+x^2-20x\cos\alpha}} \right. \\\left \{ {{40x\cos\alpha=4x^2+64\ |:40x} \atop {x^2-20x\cos\alpha+84=0}} \right. \\\left \{ {{\cos\alpha=\frac{4x^2+64}{40x}} \atop {x^2-20x\cos\alpha+84=0}} \right. \\\left \{ {{\cos\alpha=\frac{x^2+16}{10x}} \atop {x^2-20x*\frac{x^2+16}{10x}+84=0}} \right.[/tex]

[tex]\left \{ {{\cos\alpha=\frac{x^2+16}{10x}} \atop {x^2-2*(x^2+16)+84=0}} \right. \\\left \{ {{\cos\alpha=\frac{x^2+16}{10x}} \atop {x^2-2x^2-32+84=0}} \right. \\\left \{ {{\cos\alpha=\frac{x^2+16}{10x}} \atop {-x^2=-52}} \right. \\\left \{ {{\cos\alpha=\frac{x^2+16}{10x}} \atop {x^2=52}} \right. \\\left \{ {{\cos\alpha=\frac{x^2+16}{10x}} \atop {x=\sqrt{52}}} \right. \\\left \{ {{\cos\alpha=\frac{x^2+16}{10x}} \atop {x=2\sqrt{13}}} \right.[/tex]

[tex]\left \{ {{\cos\alpha=\frac{(2\sqrt{13})^2+16}{10*2\sqrt{13}}} \atop {x=2\sqrt{13}}} \right.\\\left \{ {{\cos\alpha=\frac{68}{20\sqrt{13}}} \atop {x=2\sqrt{13}}} \right.\\\left \{ {{\cos\alpha=\frac{17}{5\sqrt{13}}} \atop {x=2\sqrt{13}}} \right.[/tex]

Aby policzyć pole trójkąta, policzmy sinus kąta alfa.

[tex]\sin^2\alpha+\cos^2\alpha=1\\\sin^2\alpha+(\frac{17}{5\sqrt{13}})^2=1\\\sin^2\alpha+\frac{289}{325}}=1\\\sin^2\alpha=\frac{36}{325}}\\\sin\alpha=\sqrt{\frac{36}{325}}\vee\sin\alpha=-\sqrt{\frac{36}{325}}\\\sin\alpha=\frac{6}{5\sqrt{13}}}\vee\sin\alpha=-\frac{6}{5\sqrt{13}}}[/tex]

Sinus jest dodatni, niezależnie od tego, czy kąt alfa jest ostry czy rozwarty, więc

[tex]\sin\alpha=\frac{6}{5\sqrt{13}}}[/tex]

Policzmy pole trójkąta.

[tex]P_\triangle=\frac{1}{2}*|AC|*|BC|*\sin\alpha\\P_\triangle=\frac{1}{2}*10*4\sqrt{13}*\frac{6}{5\sqrt{13}}=20\sqrt{13}*\frac{6}{5\sqrt{13}}=\frac{120\sqrt{13}}{5\sqrt{13}}=24[/tex]

1. The press report said the president had had an accident.

2. Matthew hasn't told his boss yet that he's leaving.

3. Pat's father told her she should be more polite.

4. Danny said he was going to the USA.

5. Tell your brother that you're sorry. (bez "to")

6. Mr. Stuart said a lot about the new plans. (to jest poprawne)

Odpowiedź:

5x

Szczegółowe wyjaśnienie:

Ustalajac jednomiany podobne nie patrzymy na liczby tylko na litery. Litery muszą być takie same i w dodatku w takiej samej potędze.

I gra muzyka

Pozdrawiam

P = 12*8*1/2

P = 12*4P = 48 cm²