potrzebuje na jutro pls daje 40 pkt.
-
Temat:
Matematyka -
Autor:
jaguar -
Utworzono:
1 rok temu
Odpowiedzi 1
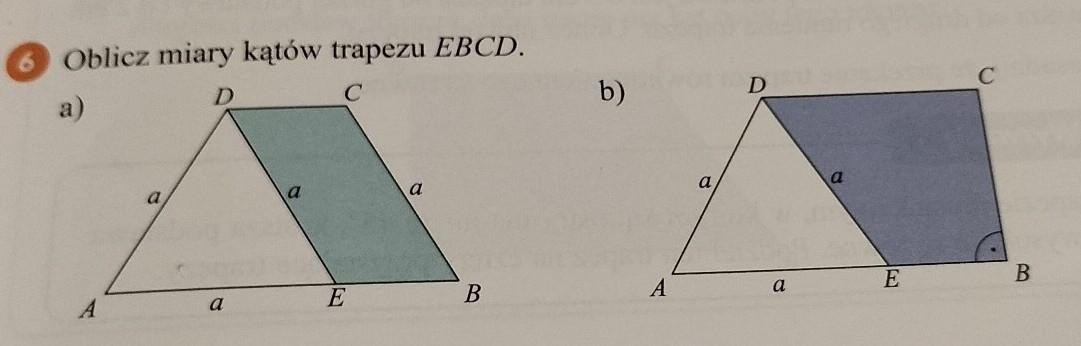
Masz w zadaniu trójkąty równoboczne wyrysowane w figurze z czego wynika ze każdy kat trójkąta ma 60 stopni W takim razie jeśli w przypadku a) wyniesiesz wysokość trapezu z boku D masz kąt prosty czyli 90 stopniW tym samym czasie podzieliłaś kąt trójkąta równobocznego na 2 części więc masz 30 Stopni po każdej stronie wysokości 90-30=60 Kąt D w równoległoboku (trapezie) EBCD ma miarę 60 stopni w takim razie po drugiej stronie (kąt B) tez ma miarę 60 stopni 60+60 daje nam 120 360-120=240/:2=120Kąt C i kąt E maja miarę 120 stopniTeraz kolej na przykład b) gdzie mamy trapez prostokątny czyli kąt B i C maja 90 stopni Kąt D robimy analogicznie do wcześniejszego zadania z czego wynika ze ma on 60 stopni Teraz wystarczy wszystko dodać i odjąć od 360 90+90+60=240360-240=120 Kąt E ma miarę 120 stopni. Proszę myślę że pomogłam;)
-
Autor:
nikopruitt
-
Oceń odpowiedź:
7
Znasz odpowiedź? Dodaj ją tutaj!
Wybierz język i region
How much to ban the user?
1 hour
1 day
100 years