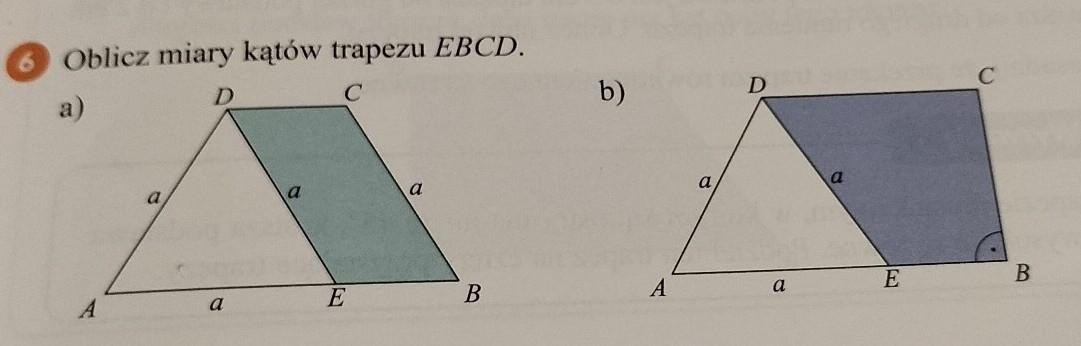
POMOCY Na trójkącie równoramiennym ABC, w którym |AC| = |BC| opisano okrąg o środku S. Wyznacz miary katów tego trójkąta, jeśli wiadomo że kąt BAS ma miarę 20 stopni.
-
Temat:
Matematyka -
Autor:
feliciano -
Utworzono:
1 rok temu
Odpowiedzi 1
Odpowiedź:
∢BAC = ∢ABC = 70º to ∢ACB = 40º
Szczegółowe wyjaśnienie:
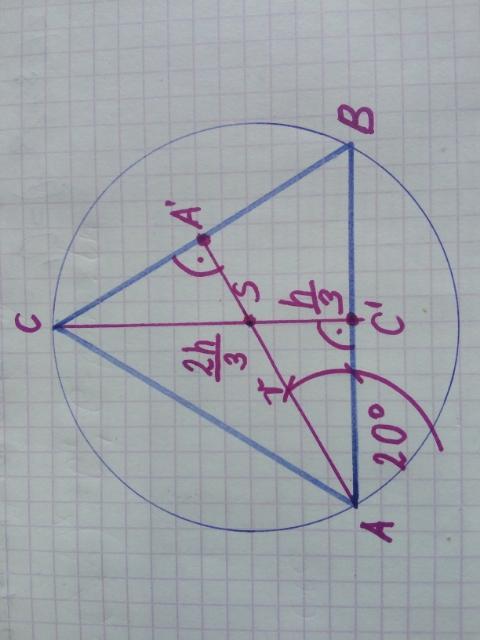
(ilustracja graficzna do zadania - załacznik)
Mamy trójkąt równoramienny a z tego wynikają szczególne zależności:
- odcinki |CC'| i |AA'| są symetralnymi boków, ponieważ środek okręgu opisanego na trójkącie S - znajduje się na przecięciu symetralnych boków: [Symetralna boku jest do boku prostopadła i dzieli bok na połowę].
Wniosek: Trójkąt ABA' jest trójkątem prostokątnym - to z sumy kątów
w każdym trójkącie mamy: ∢ABC + 20º + 90º = 180º to
∢ABC = 180º - 20º - 90º to ∢ABC = 70º to dalej,
w trójkącie równoramiennym kąty przy podstawie są równe,
to: Odpowiedź:
∢BAC = ∢ABC = 70º to ∢ACB = 40º
-
Autor:
john488
-
Oceń odpowiedź:
0
Znasz odpowiedź? Dodaj ją tutaj!
Other related questions that may help you
-
Autor:
asunción
-
Autor:
mombodkirp
-
Oceń odpowiedź:
3
-
Autor:
madison2
-
Autor:
bronsonridl
-
Oceń odpowiedź:
3