wielomiany matematyka na dzisiaj pls

question img

Odpowiedzi 2

Odpowiedź:

6. D.7. C.8. x = -4

Szczegółowe wyjaśnienie:

Zad.6D. x(5x² - 4x - 1) = 0

podstawiamy x = -5:

L = -5 · (5 · (-5)² - 4 · (-5) - 1) = -5 · (5 · 25 + 20 - 1) = -5 · (125 + 19)

= - 5 · 144 = -720

P = 0

L ≠ P

Zad.7

w(x) = x⁴ + 3x³ - 8x² - 12x + 16 =  x⁴ - 8x² + 16 + 3x³  - 12x

= (x²)² - 2 · x² · 4 + 4² + 3x(x² - 4)

stosujemy wzór skróconego mnożenia: (a - b)² = a² - 2ab + b²

= (x² - 4)² + 3x(x² - 4) = (x² - 4)(x² - 4 + 3x) = (x² - 2²)(x² + 4x - x - 4)

stosujemy wzór skróconego mnożenia: (a - b)(a + b) = a² - b²

= (x - 2)(x + 2)[x(x + 4) - 1(x + 4)] = (x - 2)(x + 2)(x + 4)(x - 1)

Z postaci iloczynowej tego wielomianu wnioskujemy, że jest on podzielny przez dwumiany:

x - 2, x + 2, x + 4 i x - 1

Czyli nie jest podzielny przez dwumian (x - 4) ⇒ C.

Zad.8

w(z) = 2x³ + 2x² - 23x + 4

Możliwe pierwiastki całkowite: { ±4, ±2, ±1} - dzielniki wyrazu wolnego.

Sprawdzamy

x = -4

w(-4) = 2 · (-4)³ + 2 · (-4)² - 23 · (-4) + 4 = 2 · (-64) + 2 · 16 + 92 + 4

= -128 + 32 + 92 + 4 = 0

Czyli liczba -4 jest pierwiastkiem tego wielomianu.

x = -4

Na mocy twierdzenia Bézouta, wielomian w(x) jest podzielny przez dwumian (x + 4).

Dzielenie wykonamy schematem Hornera (załącznik).

Czyli:

w(x) = (x + 4)(2x² - 6x + 1)

Znajdujemy pozostałe miejsca zerowe:

2x² - 6x + 1 = 0

a = 2, b = -6, c = 1

Δ = b² - 4ac

Δ = (-6)² - 4 · 2 · 1 = 36 - 8 = 28

√Δ = √28 = √(4 · 7) = 2√7

x₁ = (-b - √Δ)/(2a)

x₂ = (-b + √Δ)/(2a)

x₁ = (-(-6) - 2√7)/(2 · 2)

x₁ = (6 - 2√7)/4

x₁ = (3 - √7)/2

x₂ = (-(-6) + 2√7)/(2 · 2)

x₂ = (6 + 2√7)/4

x₂ = (3 + √7)/2

-4 < (3 - √7)/2 < (3 + √7)/2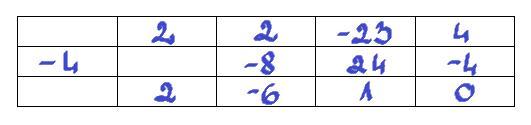
answer img

W załączniku. Liczę na NAJ.

:)

answer img

Znasz odpowiedź? Dodaj ją tutaj!

Can't find the answer?

Other related questions that may help you

Rozstrzygnij, czy wyobrażenie autora obrazu, którego reprodukcje zamieszczono poniżej, dotyczące uzbrojenia oraz wyposażenia przedstawionych postaci, odpowiada prawdzie historycznej. Wymień nieścisłości i napisz, jak powinny wyglądać poszczególne osoby.
question img

Wyobrażenie autora obrazu nie odpowiada prawdzie historycznej.

Na obrazie widać następujące nieścisłości:
  • Wichman nie powinien trzymać sztyletu, ponieważ ta krótka broń biała upowszechniła się dopiero w XIV wieku,
  • stroje postaci przedstawionych na obrazie nie odpowiadają faktycznym ubraniom noszonym w X wieku,
  • tło, na którym widać wiele namiotów wojskowych również nie odpowiada stylowi prowadzenia walk w X wieku,
  • żołnierze w tle nie powinni trzymać pik, ponieważ ta broń drzewcowa upowszechniła się dopiero w XV wieku,
Jak powinny wyglądać postacie na obrazie?
  • Mieszko I powinien mieć na sobie książęce szaty oraz hełm o owalnym kształcie,
  • Wichman również powinien mieć szaty odpowiadające możnowładcy z X wieku,
  • natomiast wojowie w tle powinni posiadać włócznie, topory albo łuki,
  • powinni też nosić drewniane tarcze ze skórzanymi zdobieniami i skórzane elementy stroju,

#SPJ1

1. Które wyrazy pasują do różnych znaczeń wyrazu rola? Zapisz je w odpowiednim miescu rola jako pole traktor rola jako zadanie akto aktor orać scenariusz rolnik grać Jakie wyrazy można podać w poniższych przykładach? Zapisz kilka rzeczowników,​

Odpowiedź:

Wyjaśnienie:

rola jako pole- traktor, rolnik, orać, siać, plony, sadzić

rola jako zadanie - polecenie, rozkaz, projekt

rola jako gra- aktor, scenariusz, grać, udawać

Ciało spadające z pewnej wysokości zderza się z powierzchnią Ziemi z prędkością 50 m/s. Jak długo trwało spadanie tego ciała? Prosze o szybką pomoc

[tex]Dane:\\v_{o} = 0\\v = 50\frac{m}{s}\\g = 10\frac{m}{s^{2}}\\Szukane:\\t = ?[/tex]

Wartość prędkości ciała osiągnięta po czasie t przez ciało, które poruszało się ruchem prostoliniowym jednostajnie przyspieszonym, jeśli w chwili początkowej spoczywało:

[tex]v = a\cdot t\\\\a = g\\\\zatem\\\\v = g\cdot t \ \ \ /:g\\\\t = \frac{v}{g}\\\\t = \frac{50\frac{m}{s}}{10\frac{m}{s^{2}}}\\\\\boxed{t = 5 \ s}[/tex]

Odp. Spadanie ciała trwało 5 sekund.

eatujcielwlqfwwwhsqueiee
question img

Zadanie 4:

1/10 -> dęby

3/10 -> brzozy

4/10 -> topole

1 - (1/10 - 3/10 - 4/10) = 1 - 8/10 = 2/10 -> modrzewia i jodły

drzewa liściaste -> 1/10 + 3/10 + 4/10 = 8/10

drzewa iglaste -> 1 - 8/10 = 2/10

Zadanie 5:

a) 2  2/3 + 1/3 + 2  4/5 = 3 + 2  4/5 = 5  4/5

b) 7/9 + 1  3/4 + 1/4 = 7/9 + 2 = 2  7/9

c) 2  5/7 + 2  2/7 + 7  2/5 + 3  3/5 = 8 + 11 = 19

d) 2  3/4 + 1  2/4 + 1  1/6 + 4  5/6 = 3  5/4 + 6 = 4  1/4 + 6 = 10  1/4

:)

Odpowiedź:

Szczegółowe wyjaśnienie:

liściaste

dęby - 1/10

brzozy - 3/10

topole - 4/10

1/10+3/10+4/10=8/10=4/5

iglaste

1 -4/5=5/5-4/5=1/5----modrzew i jodła

_______________________

=3+2 4/5 =5 4/5

= 7/9 +2= 2 7/9

=4 7/7+10 5/5= 5 +11 =16

= 3 5/4 + 5 6/6=4 1/4 +6 =10 1/4

________________________

x=4 -3 5/7

x=3 7/7-3 5/7

x=2/7

y=1 -5/9

y=9/9 -5/9

y=4/9

x=5- 3 8/10

x=5 -3 4/5

x=4 5/5 -3 4/5

x=1 1/5

Other Matematyka Questions

Zaloguj się z Google

 lub

Zapomniałeś(aś) hasła?

Nie mam jeszcze konta, ale chcę je założyć Zarejestruj się

Wybierz język i region

English

United States

Polski

Polska

Português

Brasil

English

India

English

Philippines

Español

España

Bahasa Indonesia

Indonesia

Türkçe

Türkiye
How much to ban the user?
1 hour 1 day 100 years