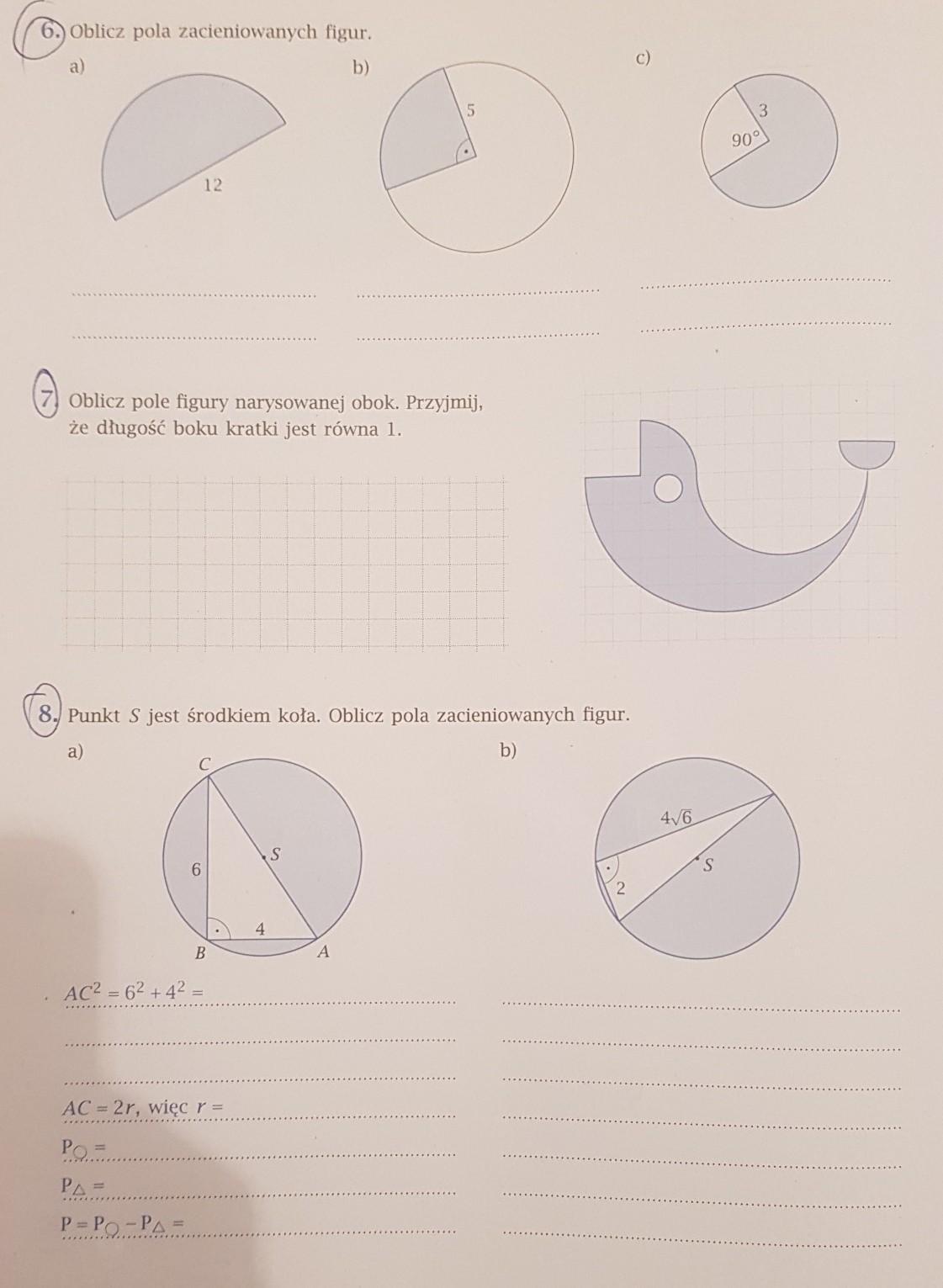
Oblicz pole trójkąta równobocznego którego wysokość wynosi 4√5
-
Temat:
Matematyka -
Autor:
jesse63 -
Utworzono:
1 rok temu
Odpowiedzi 2
Odpowiedź:
h = a*[tex]\frac{\sqrt{3} }{2}[/tex] = 4 √5 /* [tex]\frac{2}{\sqrt{3} }[/tex]
a = [tex]\frac{8\sqrt{5} }{\sqrt{3} }[/tex]
P = 0,5 a*h = 0,5* [tex]\frac{8 \sqrt{5} }{\sqrt{3} } *4\sqrt{5}[/tex] = [tex]\frac{80}{\sqrt{3} }[/tex] = [tex]\frac{80}{3} \sqrt{3}[/tex]
Szczegółowe wyjaśnienie:
-
Autor:
brooklyn0tcc
-
Oceń odpowiedź:
7
Szczegółowe wyjaśnienie:
[tex]h=4\sqrt{5}[/tex]
1.Korzystając ze wzoru na wysokość trójkąta równobocznego obliczamy
długość boku a
[tex]h=\frac{a\sqrt{3} }{2}[/tex] ← wysokość w trójkącie równobocznym o boku a
[tex]\frac{a\sqrt{3} }{2} =4\sqrt{5}[/tex] [tex]/*2[/tex]
[tex]a\sqrt{3} =8\sqrt{5}[/tex] [tex]/:\sqrt{3}[/tex]
[tex]a=\frac{8\sqrt{5} }{\sqrt{3} }[/tex]
usuwamy niewymierność w mianowniku
[tex]a=\frac{8\sqrt{5} }{\sqrt{3} }*\frac{\sqrt{3} }{\sqrt{3} } =\frac{8\sqrt{15} }{3}[/tex]
[tex]a=\frac{8\sqrt{15} }{3}[/tex]
2. Obliczamy pole trójkąta równobocznego P
[tex]P=\frac{a^{2} \sqrt{3} }{4}[/tex] ← wzór na pole trójkąta równobocznego o boku a
[tex]P=\frac{(\frac{8\sqrt{15} }{3})^{2}\sqrt{3} }{4} =[(\frac{64*15}{9} )\sqrt{3}] *\frac{1}{4} =[\frac{960\sqrt{3} }{9} ]*\frac{1}{4} =\frac{240\sqrt{3} }{9} =\frac{80\sqrt{3} }{3}[/tex]
Pole trójkąta wynosi [tex]\frac{80\sqrt{3} }{3}[/tex]
-
Autor:
kyanzw7p
-
Oceń odpowiedź:
6
Znasz odpowiedź? Dodaj ją tutaj!
Other related questions that may help you
-
Autor:
emilio
-
Autor:
rabbitpmns
-
Oceń odpowiedź:
3
-
Autor:
faithatab
-
Oceń odpowiedź:
8
-
Autor:
braylon
-
Autor:
alannahfhtv
-
Oceń odpowiedź:
0
-
Autor:
veronicaschultz
-
Autor:
dottienscb
-
Oceń odpowiedź:
6