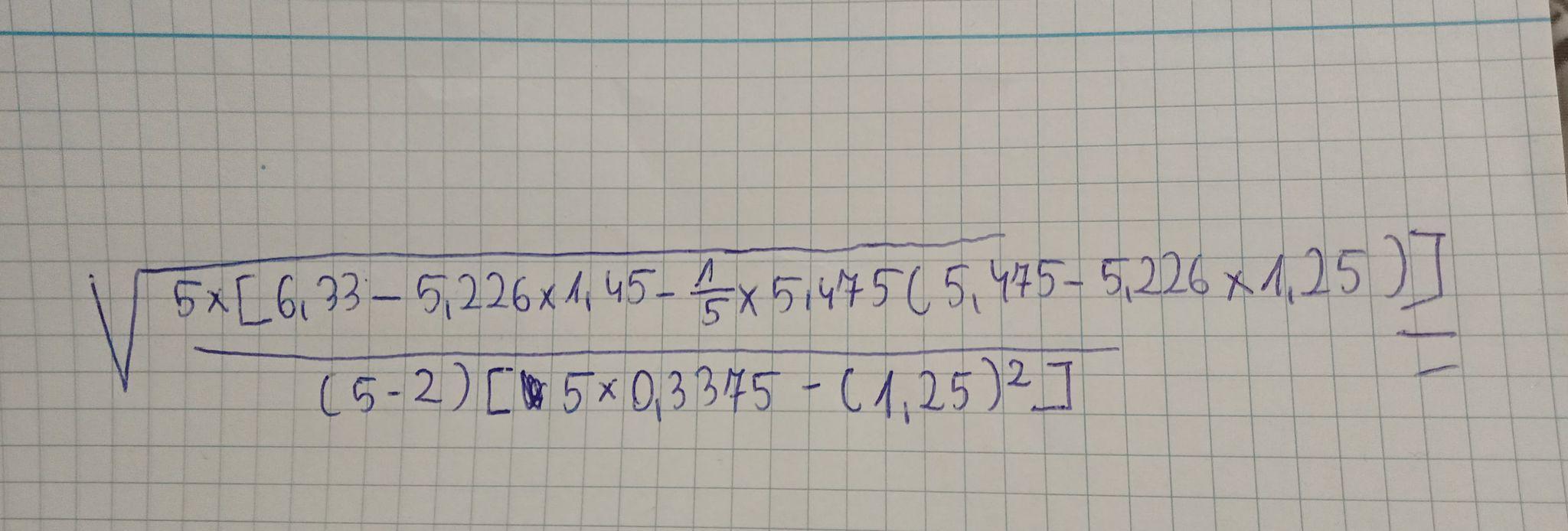naszkicuj wykres funkcji f(x)=|x+2|+3 korzystając z wykresu funkcji y=|x|
-
Temat:
Matematyka -
Autor:
zavier -
Utworzono:
1 rok temu
Odpowiedzi 1
Odpowiedź:
Wykres w załączniku.Szczegółowe wyjaśnienie:
Przekształcenia wykresu funkcji f(x):f(x) + n - przesunięcie o n jednostek w górę
f(x) - n - przesuniecie o n jednostek w dół
f(x + n) - przesunięcie o n jednostek w lewo
f(x - n) - przesunięcie o n jednostek w prawo
-f(x) - symetria osiowa względem osi OX
f(-x) - symetria osiowa względem osi OY
|f(x)| - symetria częściowa względem osi OX dla y < 0
f(|x|) - symetria częściowa względem osi OY dla x > 0
Mamy funkcję:
f(x) = |x + 2| + 3y = |x|⬇ T[-2, 0] - translacja (przesunięcie) o dwie jednostki w lewo
y = |x + 2|⬇ T[0, 3] - translacja (przesunięcie) o trzy jednostki w górę
y = |x + 2| + 3Złożenie tych przekształceń daje nam T[-2, 3] - translacja (przesunięcie) o dwie jednostki w lewo i trzy jednostki w górę.
Aby narysować wykres y = |x|. Należy narysować wykres y = x i odbić symetrycznie część prostej znajdującej się poniżej osi OX względem tej osi.
Do narysowania wykresu funkcji liniowej, który jest prostą, wystarczą nam dwa punkty.
Wybieramy dowolną wartość x i obliczamy y:
dla x = 0
y = 0
(0, 0)dla x = 2
y = 2
(2, 2)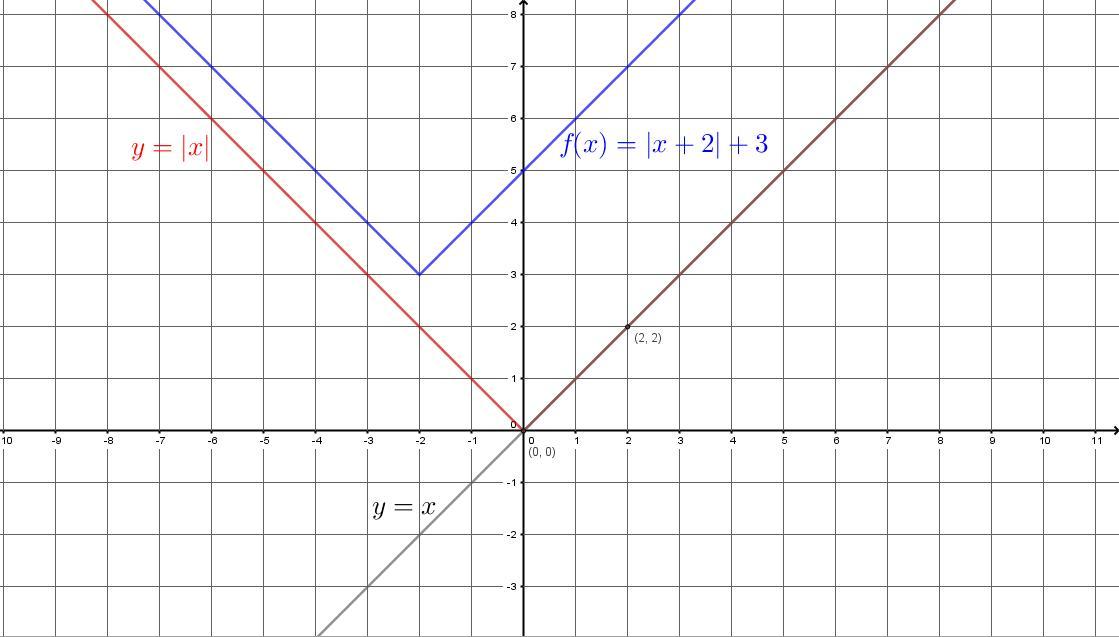
-
Autor:
paytontrqg
-
Oceń odpowiedź:
4
Znasz odpowiedź? Dodaj ją tutaj!
Other related questions that may help you
-
Autor:
kelley
-
Autor:
pippinpace
-
Oceń odpowiedź:
7
-
Autor:
alyviaritter
-
Oceń odpowiedź:
5
