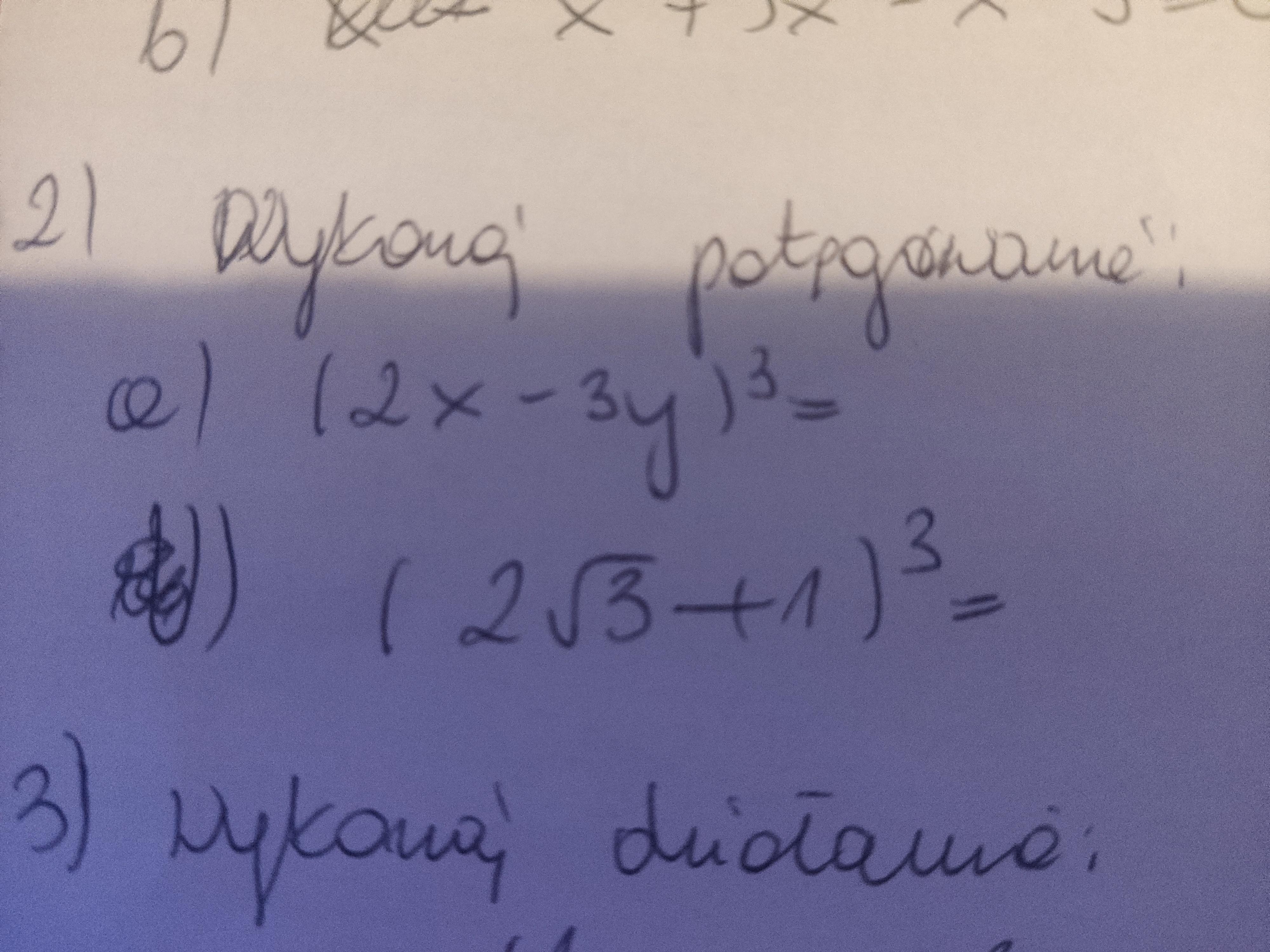rozwiąż równanie [tex]-x^2+42x-378=0[/tex]
-
Temat:
Matematyka -
Autor:
rolandcalhoun -
Utworzono:
1 rok temu
Odpowiedzi 2
[tex] - {x}^{2} + 42x - 378 = 0[/tex]
dzielę obie strony przez -1
[tex] {x}^{2} - 42x + 378 = 0[/tex]
liczę deltę (trójkąt, ale nie wiem jak tu wstawić)
[tex]delta = {b}^{2} - 4ac[/tex]
[tex]delta = 1764 - 4 \times 1 \times 378 = 1764 - 1512 = 252[/tex]
[tex] \sqrt{delta} = \sqrt{252} = \sqrt{36 \times 7} = 6 \sqrt{7} [/tex]
[tex]x \frac{}{1} = \frac{ - b - \sqrt{delta} }{2a} = \frac{42 - 6 \sqrt{7} }{2} = \frac{2(21 - 3 \sqrt{7}) }{2} = 21 - 3 \sqrt{7} [/tex]
[tex]x \frac{}{2} = \frac{ - b + \sqrt{delta} }{2a} = \frac{42 + 6 \sqrt{7} }{2} = \frac{2(21 + 3 \sqrt{7}) }{2} = 21 + 3 \sqrt{7} [/tex]
Odp. Są dwa rozwiązania tego równania x1 i x2 (wyżej jest podana ich wartość).
-
Autor:
lexivwti
-
Oceń odpowiedź:
15
Odpowiedź:
Szczegółowe wyjaśnienie:
-x²+42x-378=0
Δ=b²-4ac
Δ=42²-4*(1)*(-378)=1764-1512=252
√Δ=√252=6√7
x1=-b-√Δ/2a
x1=-42-6√7/-2=21+3√7
x2=-b+√Δ/2a
x2=-42+6√7/-2=21-3√7
-
Autor:
areli6n1q
-
Oceń odpowiedź:
0