Na rysunku obok przedstawiono wykresy funkcji f(x)= -[tex]\frac{1}{4}[/tex][tex]x^{2}[/tex] + [tex]\frac{1}{3}[/tex]x + 2 i g(x)= [tex]x^{2}[/tex] - 6x + 8.Korzystając z tych wykresów, podaj rozwiązanie nierówności.a) -[tex]\frac{1}{3}[/tex][tex]x^{2}[/tex] + [tex]\frac{1}{3}[/tex]x + 2 [tex]\geq[/tex] 0b) -[tex]\frac{1}{3}[/tex]x + 2 [tex]\leq[/tex] 0DAJE NAJ!!
-
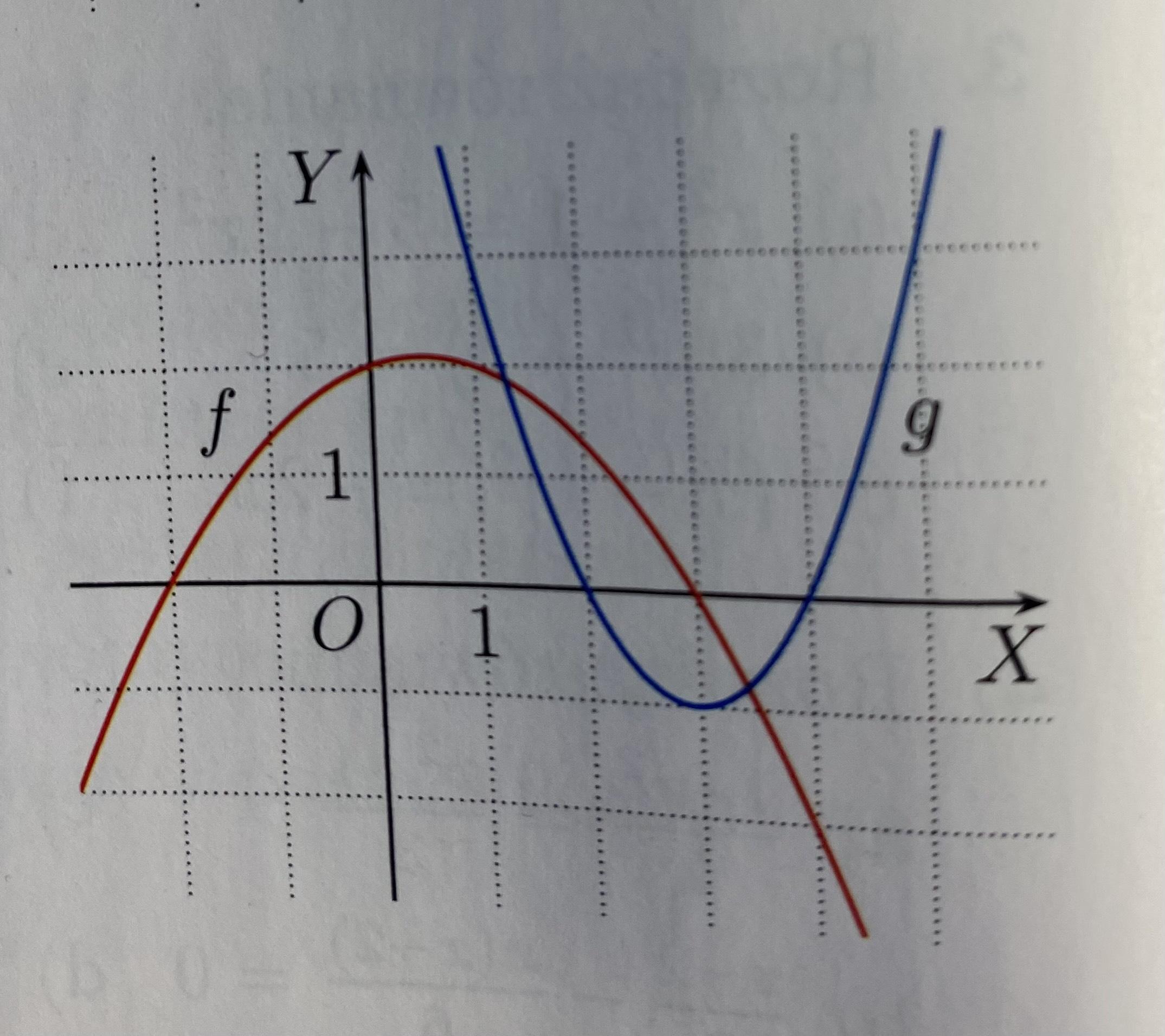
Temat:
Matematyka -
Autor:
dylan17 -
Utworzono:
1 rok temu
Odpowiedzi 1
a) Δ = [tex](\frac{1}{3}) ^{2}[/tex] - 4 * [tex](-\frac{1}{3} )[/tex] * 2 = [tex]\frac{1}{9}\\[/tex] + [tex]\frac{24}{9}[/tex] = [tex]\frac{25}{9}[/tex]
sqrt(Δ) = [tex]\frac{5}{3}[/tex]
[tex]x_{1}[/tex] = [tex]\frac{-\frac{-1}{3} + \frac{5}{3} }{2 * \frac{1}{3} }[/tex] = 3 [tex]x_{2} =\frac{-\frac{-1}{3} - \frac{5}{3} }{2 * \frac{1}{3} }[/tex] = [tex]-\frac{4}{3} *\frac{3}{2}=-2[/tex]
x∈(-∞,-2>∪<3,∞)
b) Δ = [tex]\frac{8}{3}[/tex]
sqrt(Δ) = [tex]\sqrt{ \frac{8}{3} }[/tex]
[tex]x_{1\\}[/tex]= [tex]-\sqrt{\frac{8}{4*3} }=-\sqrt{\frac{2}{3} }[/tex] [tex]x_{\\2}[/tex]=[tex]\sqrt{\frac{8}{4*3} }=\sqrt{\frac{2}{3} }[/tex]
x∈<[tex]-\sqrt{\frac{2}{3} }[/tex],[tex]\sqrt{\frac{2}{3} }[/tex]>
mam nadzieję że dobrze i przepraszam jeżeli wychodzę poza program, inaczej nie umiem
-
Autor:
preciousvalentine
-
Oceń odpowiedź:
0
Znasz odpowiedź? Dodaj ją tutaj!
Other related questions that may help you
-
Autor:
ean
-
Autor:
dunndominguez
-
Oceń odpowiedź:
5
-
Autor:
finleykaks
-
Oceń odpowiedź:
7
-
Autor:
louis
-
Autor:
teresachang
-
Oceń odpowiedź:
9
-
Autor:
jasmine
-
Autor:
ebonygraves
-
Oceń odpowiedź:
0
-
Autor:
edwards
-
Autor:
lincoln362
-
Oceń odpowiedź:
1