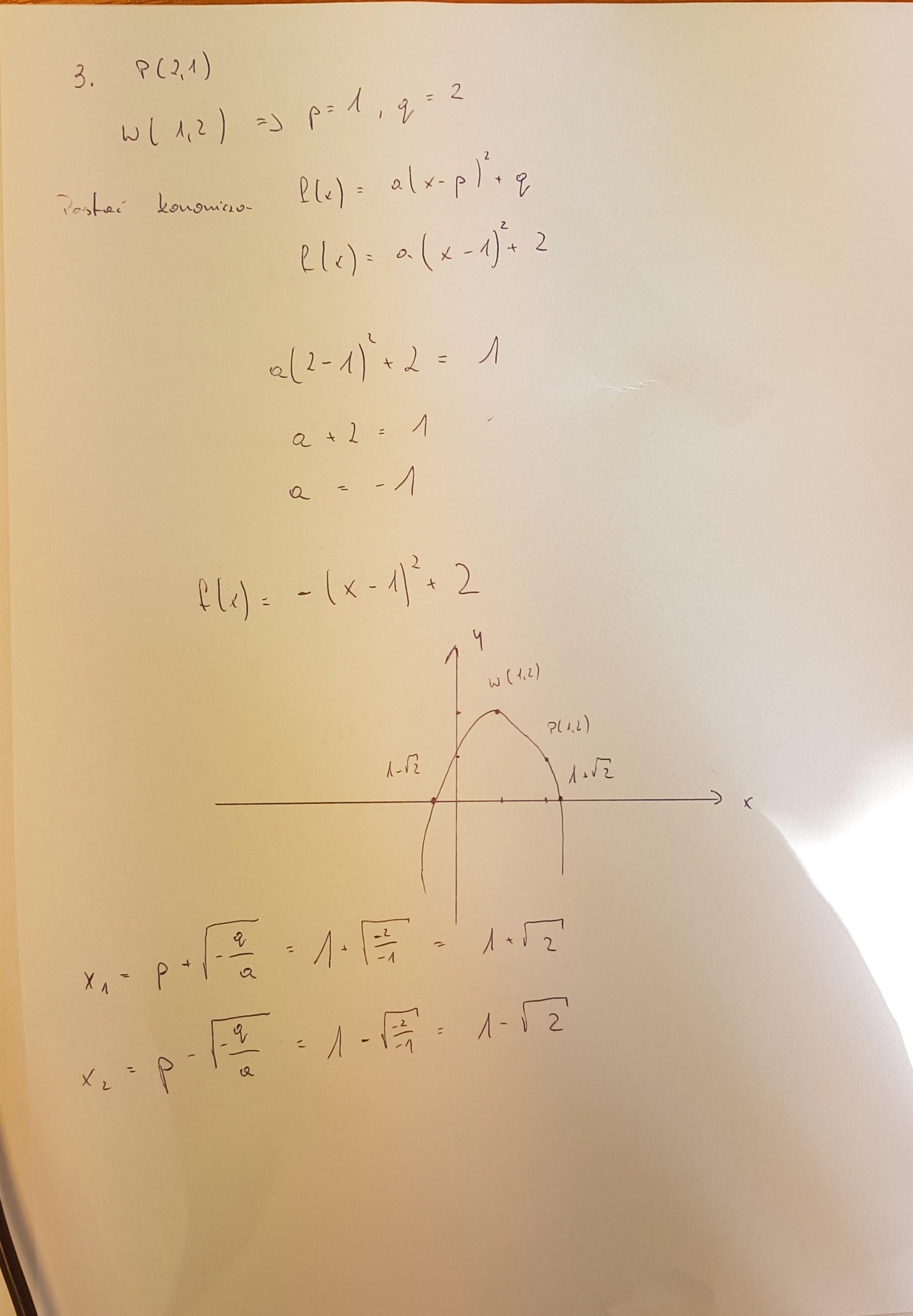Proszę o rozwiązanie zadań, nie tylko abc, ale też działania



-
Temat:
Matematyka -
Autor:
barney -
Utworzono:
1 rok temu
Odpowiedzi 1
Odpowiedź:
Szczegółowe wyjaśnienie:
z.1
[tex]\frac{1}{3}-0.(3)=0\\-\sqrt{3}+1\frac{7}{9}=-\sqrt{3}+\frac{16}{9}=-\sqrt{\frac{3\cdot81}{81}}+\sqrt{\frac{16\cdot16}{81}}=-\sqrt{\frac{243}{81}}+\sqrt{\frac{256}{81}} =\frac{-\sqrt{243}+\sqrt{256}}{9} =(*)[/tex]
(*) jest większe od zera, bo [tex]\sqrt{256}-\sqrt{243} > 0[/tex]
Więc odpowiedź B.
z.2
Proporcje(mnożenie na krzyż):
20 -------- 62.5%
x ----------- 37.5%
[tex]20\cdot37.5\%=x\cdot62.5\%\iff x=20\cdot\frac{37.5}{62.5}= 20 \cdot\frac{75}{125}=20\cdot\frac{3}{5}=4\cdot3=12[/tex]
B.12
z.3
[tex]a=3log_{8}4=log_{8}4^3=log_{8}(2^2)^3=log_{8}(2^3)^2=2\cdot log_{8}2^3=2\cdot log_{8}8=2\cdot 1 = 2[/tex]
Trzeba pamiętać, że
[tex]log_ab^c=c\cdot log_ab\\log_aa=1[/tex]
a>0 i a!=1
C.2
z.4
[tex](3-\sqrt{5})^2=3^2-2\cdot3\cdot\sqrt{5}+(\sqrt{5})^2=9-6\sqrt{5}+5=14-6\sqrt{5}[/tex]
C.[tex]14-6\sqrt{5}[/tex]
z.5
[tex]5^{100}+5^{100}+5^{100}+5^{100}+5^{100}=5\cdot5^{100}=5^{101}[/tex]
Odpowiedź B.
z.6
x = 100%x - cena początkowa towaru
Najpierw obniżka o 30% od pierwotnej ceny:
100%x-30%*x=70%*x
Później obniżka o 20% od późniejszej ceny(czyli z tych 70%*x)
70%x-20%*70%x=70%x-14%x=56%x
O ile obniżono cenę towaru?
Na początku było 100%, a teraz jest 56%. Zatem obniżono o 44%.
Odpowiedź D. 44%
z.7
Z treści zadania wynika, że (6/x)=((6-2)/(x-3)):
[tex]\frac{6}{x}=\frac{6-2}{x-3}=\frac{4}{x-3}\\6\cdot(x-3)=4x\iff 6x-18=4x\iff 6x-4x=18 \iff 2x=18 \iff x=9[/tex]
Pierwotny ułamek: [tex]\frac{6}{9}[/tex]
Odpowiedź D.[tex]\frac{6}{9}[/tex]
z.8
[tex]K_n=K\cdot(1+\frac{p}{100})^n\\\\\verb|p - oprocentowanie w skali rocznej|\\\verb|n - liczba lat kapitalizacji|\\[/tex]
Odsetki kapitalizują się co pół roku, czyli to jest oprocentowanie 6% w skali pół roku.
U nas:
[tex]\verb|K=500|\\\verb|n=4|\\\verb|p=6%/2=3%|\\K_4=500\cdot(1+\frac{3}{100})^{4}=500\cdot(1.03)^4[/tex]
Odpowiedź D.
z.9
[tex]5\frac{3}{11}-2\frac{1}{11}\cdot\sqrt[3]{-8}=\frac{58}{11}+\frac{23\cdot2}{11}=\frac{104}{11}[/tex]
odwrotność, czyli licznik z mianownikiem się zamieniają miejscami
[tex](\frac{104}{11})^{-1}=\frac{11}{104}[/tex]
Odpowiedź B.[tex]\frac{11}{104}[/tex]
z.10
[tex]\sqrt[3]{3}\cdot \sqrt[6]{3}=(3)^{\frac{1}{3}}\cdot(3)^{\frac{1}{6}}=3^{(\frac{1}{3}+\frac{1}{6})}=3^{\frac{3}{6}}=3^{\frac{1}{2}}=\sqrt{3}[/tex]
Odpowiedź D.[tex]\sqrt{3}[/tex]
z.11
[tex]log_{2}(log20+log5)=log_{2}(log(20\cdot5))=log_2(log100)=log_2(log10^2)=log_2(2\cdot log10)=log_2(2\cdot 1)=log_22=1[/tex]
Skorzystałem z tego, że
[tex]log_ab+log_ac=log_a(b\cdot c)\\log_aa=1[/tex]
A, i jak nie ma podstawy logarytmu napisanej(ta malutka liczba na dole logarytmu) to zakładamy, że podstawa wynosi '10'.
Odpowiedź C.1
z.12
[tex]2x-4<10 \iff 2x < 14 \iff x < 7\\x \in (-\infty, 7)[/tex]
Odpowiedź A.
z.13
[tex]2\sqrt{50}-4\sqrt{8}=2\sqrt{5^2\cdot2}-4\sqrt{2^2\cdot 2}=2\cdot 5\sqrt{2}-4\cdot 2\sqrt{2}=10\sqrt{2}-8\sqrt{2}=2\sqrt{2}=2^1\cdot 2^{\frac{1}{2}}=2^{\frac{3}{2}}[/tex]
Odpowiedź A.
z.14
Wartość bezwzględna z x:
[tex]|x|=|\frac{(\frac{3}{2})^2-\frac{1.2}{4.8}}{\frac{-7}{3}\cdot\frac{1}{7}}| = |\frac{\frac{9}{4}-\frac{1}{4}}{-\frac{1}{3}}|=|\frac{\frac{8}{4}}{-\frac{1}{3}}|=|\frac{2}{-\frac{1}{3}}|=2\cdot 3 = 6[/tex]
Odpowiedź B.6
z.15
Lecimy po kolei:
[tex](0.1)^{-3}=(\frac{1}{10})^{-3}=10^{3}=1000 > 1[/tex]
Odpowiedź A.
z.16
[tex](\frac{3}{5})^5\cdot(\frac{5}{3})^4=\frac{3^5}{5^5}\cdot \frac{5^4}{3^4}=\frac{3}{5}[/tex]
Odpowiedź C.
z.17
[tex]\frac{\frac{3}{4}-\frac{2}{3}}{\frac{2}{3}-\frac{1}{2}} = \frac{\frac{3\cdot3-2\cdot4}{12}}{\frac{2\cdot2-1\cdot3}{6}}=\frac{\frac{1}{12}}{\frac{1}{6}}=\frac{6}{12}=\frac{1}{2}[/tex]
Odpowiedź B.
z.18
[tex]x^{0.1205}=6\\x^{0.3615}=?\\x^{0.3615}=(x^{0.1205})^{3}=6^3=216[/tex]
Odpowiedź B. 216
z.19
Jak sobie obliczysz, to:
[tex]\frac{1}{\sqrt{7}-\sqrt{6}}=5.0952410538477686886988998283451518176762066637391203088010270264...[/tex]W zaokrągleniu do 0.01 wychodzi to jakieś 5.10
Odpowiedź C.5,10
z.20
[tex]4^{log_{2}5}=(2^2)^{log_{2}5}=2^{2log_{2}5}=2^{log_{2}25}= 25[/tex]
Korzystamy tutaj tylko z tego, że:
[tex]a^{log_{a}b}=b[/tex]
z.21
[tex]|1.(41)-\sqrt{2}| = \sqrt{2}-1.(41)[/tex] <---- bo wartość bezwzględna musi być dodatnia, a pierwiastek z dwoch jest wiekszy niz 1.(41)
Odpowiedź C.
z.22
Jak na tym diagramie rozróżnić załogę i pasażerów II klasy?
Liczba podróżujących 3. klasą:
[tex]2200\cdot 0.4=880[/tex]
Załóżmy, że załoga to te 32% całkowitej liczby ludzi:
[tex]2200\cdot 0.32=704[/tex]
W poleceniu mamy określić o ile procent liczba podróżujących 3. klasą jest większa od liczby członków załogi, zatem:
[tex]\frac{880-704}{704}\cdot100\%=\frac{176}{704}\cdot100\%=25\%[/tex]
Odpowiedź B. 25%
z.23
Liczba 4 nie należy do przedziału A, bo przedział A jest prawostronnie otwarty(czyli jest bez liczby 4).
C. należy tylko do przedziału B
z.24
Hmmm, pomnóżmy ten ułamek przez specjalnie spreparowaną jedynkę(w tym przypadku chcemy pozbyć się niewymierności z mianownika, więc pomnożymy sobie dopełnieniem do wzoru skróconego mnożenia: (a-b)(a+b)=a^2-b^2, czyli w tym przypadku [tex]\frac{2+\sqrt{3}}{2+\sqrt{3}}[/tex])
[tex]\frac{x}{y}=\frac{2+\sqrt{3}}{2-\sqrt{3}}= \frac{2+\sqrt{3}}{2-\sqrt{3}}\cdot \frac{2+\sqrt{3}}{2+\sqrt{3}}=\frac{4+4\sqrt{3}+3}{4-3}=\frac{7+4\sqrt{3}}{1}=7+4\sqrt{3}[/tex]
A jak wiemy, liczba niewymierna + liczba wymierna = liczba niewymierna
Odpowiedź B. liczba niewymierna
z.25
[tex]A=(5^4)^3=5^{12}\\B=5^5+5^5=2\cdot 5^5\\C=5^{12}:5^{7}=5^{12-7}=5^5\\D=5^3\cdot5^6=5^{3+6}=5^9[/tex]
Jak można zauważyć:
[tex]5^{12} > 5^9 > 2\cdot 5^5 > 5^5[/tex]
Zatem A>D>B>C
Odpowiedź B. A>D>B>C
-
Autor:
mariannak5t1
-
Oceń odpowiedź:
5