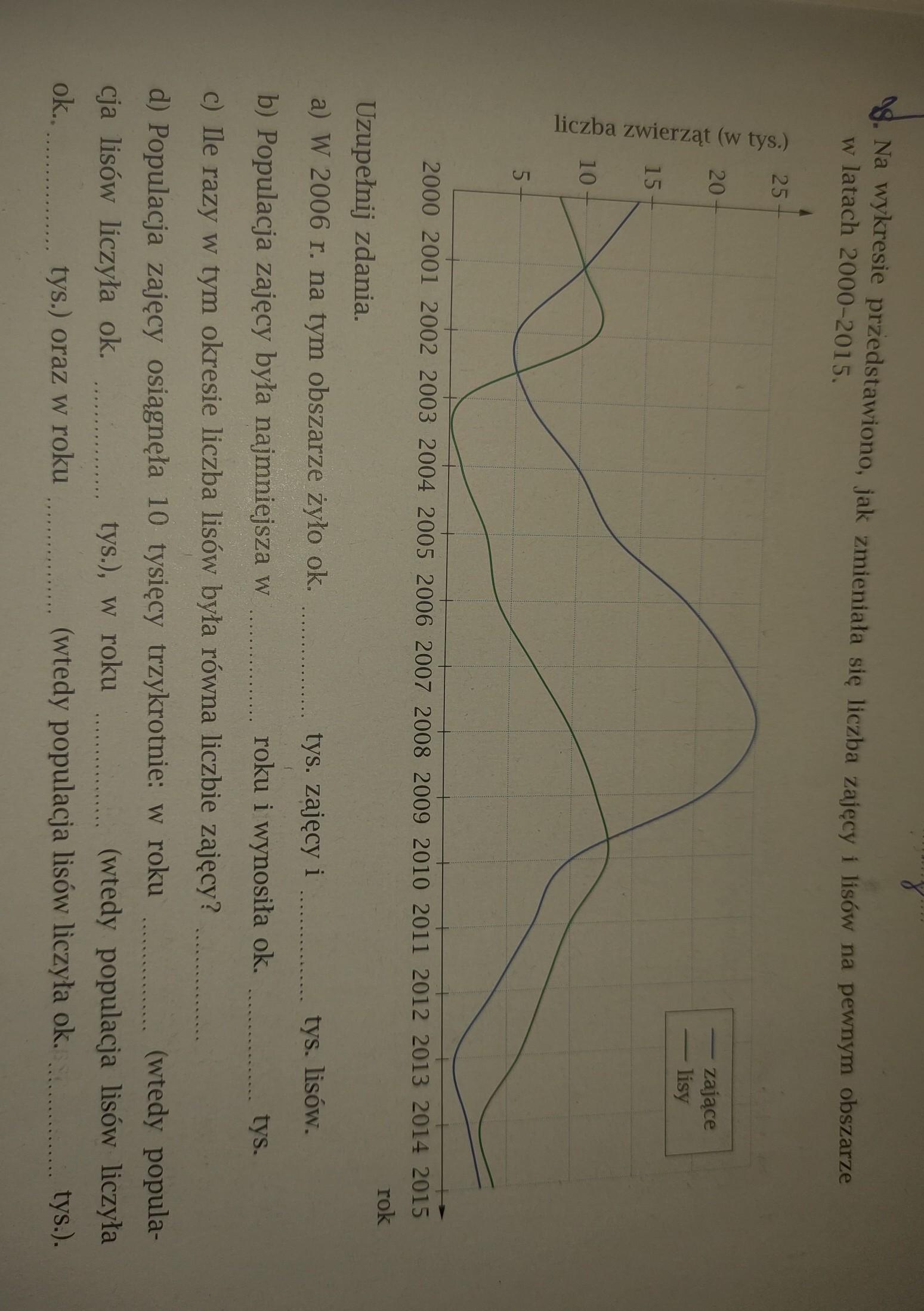
Na wykresie przedstawiono jak zmieniała się liczba zajęcy i lisów na pewnym obszarze w latach 2000-2015 a) w 2006 roku na tym obszarze żyło ok. ....... tys zajęcy i ....... tyś. lisów.b) Populacja zajęcy była najmniejsza w ....... roku i wynosiła ok. ........ tys.c) Ile razy w tym okresie liczba lisów była równa liczbie zajęcy ? .......d) Populacja zajęcy osiągnęła 10 tysięcy trzykrotnie: w roku ........(wtedy populacja lisów liczyła ok. ........ tys), w tym roku ..........( wtedy populacja lisów liczyła ok......... tys) oraz w roku ...........( wtedy populacja lisów liczyła ok........tys).Proszę o pomoc !!!Zdjęcie w załączniku.

Temat:
Matematyka
Autor:
luke39
Utworzono:
1 rok temu

Odpowiedzi 1

Odpowiedź:

a) 20 tys zajęcy i 5 tys lisówb)2013 r i 1 tys c) 3 d) 2001 10tys, 2004 1 tys, 2004 1

Autor:

winstonbmbr
Oceń odpowiedź:
7

Znasz odpowiedź? Dodaj ją tutaj!

Can't find the answer?

Other related questions that may help you

5.22 Oblicz pole rombu, którego bok ma długość 6 cm, a suma długości przekątnych jest równa 16 cm.

Autor:

alia

Autor:

nitrozmqw
Oceń odpowiedź:
1

Autor:

baldiebjih
Oceń odpowiedź:
16

BŁAGAM NA JUŻ DAJE NAJ!!!!1) Ciało poruszało się ruchem jednostajnie przyspieszonym oblicz drogę, jaką przebyło to ciało w czasie 5[s] jeżeli jego przyspieszenie było równe 5 [m/s2]. 2) Ciało poruszało się ruchem jednostajnym prostoliniowym oblicz drogę, jaką przebyło to ciało w czasie 15[s] jeżeli jego prędkość było równe 45 [m/s] . 3) Ciało poruszało się ruchem jednostajnie przyspieszonym oblicz prędkość, jaką przebyło to ciało w czasie 10[s] jeżeli jego przyspieszenie było równe 5 [m/s2] . C