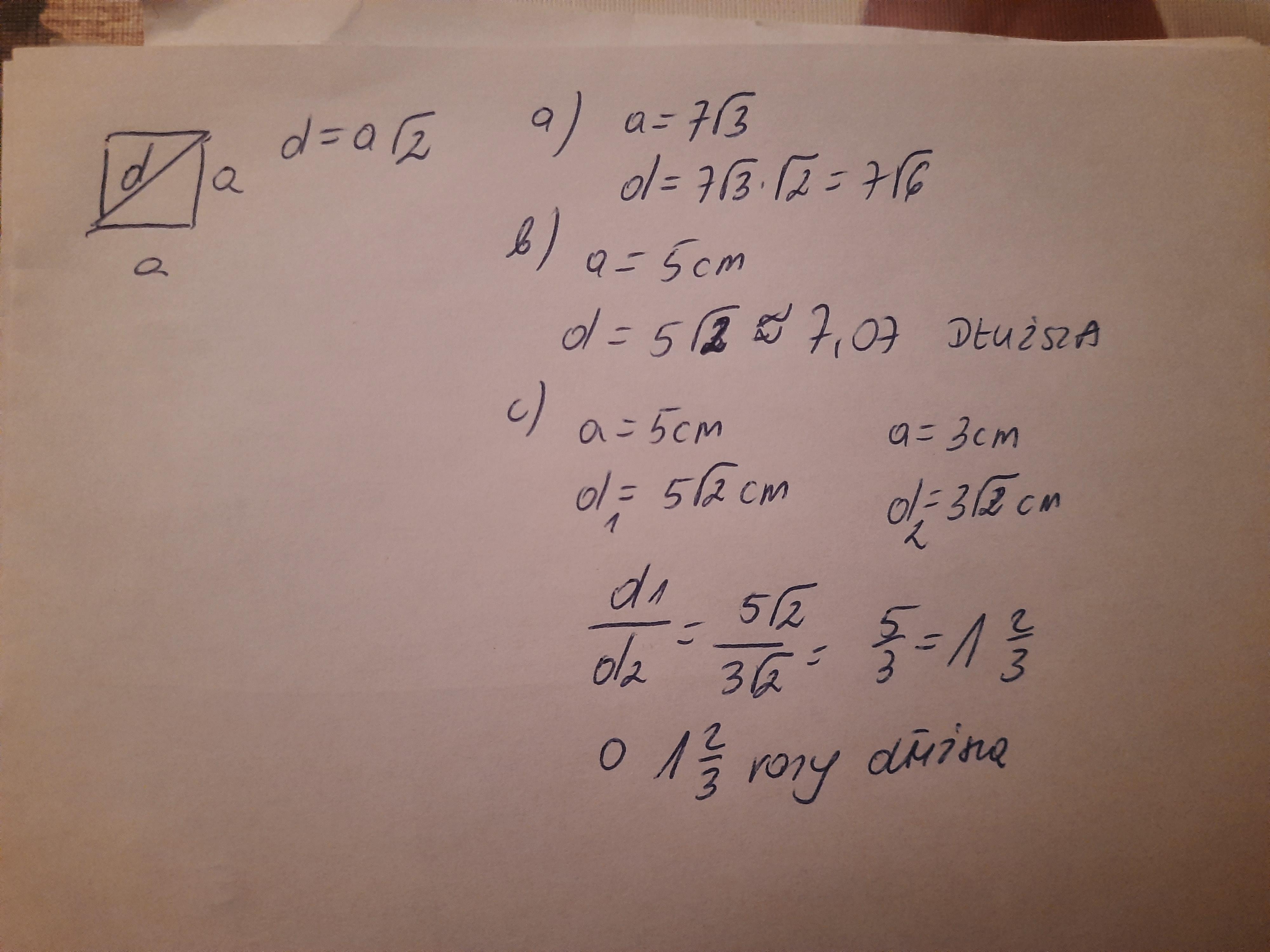zad 18,19 i 20 na jutro
-
Temat:
Matematyka -
Autor:
francisco -
Utworzono:
1 rok temu
Odpowiedzi 1
Odpowiedź:
[tex]\huge\boxed{18.\ L=32cm}\\\boxed{19.\ \text{o okolo}\ 3cm}[/tex]
Szczegółowe wyjaśnienie:
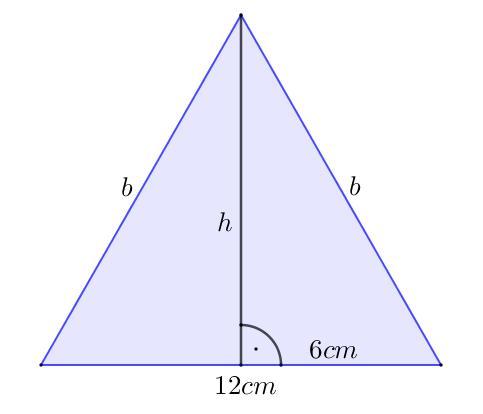
18. (patrz rysunek w załączniku).
Pole trójkąta:
[tex]P=\dfrac{a\cdot h}{2}[/tex]
Podstawiamy:
[tex]P=48cm^2,\ a=12cm\\\\48=\dfrac{12\!\!\!\!\diagup^6\cdot h}{2\!\!\!\!\diagup_1}\\\\48=6h\qquad|:6\\\\\boxed{h=8(cm)}[/tex]
Korzystamy z twierdzenia Pitagorasa:
[tex]b^2=6^2+8^2\\b^2=36+64\\b^2=100\to b=\sqrt{100}\\\boxed{b=10(cm)}[/tex]
Obliczamy obwód trójkąta:
[tex]L=12cm+2\cdot10cm=12cm+20cm=32cm[/tex]
19. Z twierdzenia Pitagorasa obliczamy długość [tex]x[/tex] deski:
3m = 300cm
[tex]x^2=300^2+30^2\\x^2=90000+900\\x^2=90900\to x=\sqrt{90900}\\x=\sqrt{900\cdot101}\\x=\sqrt{900}\cdot\sqrt{101}\\x=30\sqrt{101}\\x\approx30\cdot10,05\\\boxed{x=301,5(cm)}[/tex]
Dwie takie deski dają w sumie długość:
[tex]301,5cm\cdot2=603cm[/tex]
Szerokość sali lekcyjnej wynosi [tex]2\cdot3m=6m=600cm[/tex].
Czyli obie deski razem są za długie o [tex]603cm-600cm=3cm[/tex]
Stąd mamy odpowiedź, że jedną z desek należy skrócić o około 3cm.
-
Autor:
cassiscarroll
-
Oceń odpowiedź:
3
Znasz odpowiedź? Dodaj ją tutaj!
Other related questions that may help you
-
Autor:
robertson5
-
Autor:
ladybugwqdq
-
Oceń odpowiedź:
12
-
Autor:
glenn82
-
Autor:
cottondii9
-
Oceń odpowiedź:
14
-
Autor:
trenton554
-
Oceń odpowiedź:
2
-
Autor:
mac97
-
Autor:
shaniasagl
-
Oceń odpowiedź:
3
-
Autor:
braydon
Odpowiedź:
Szczegółowe wyjaśnienie:
-
Autor:
jetshepherd
-
Oceń odpowiedź:
1