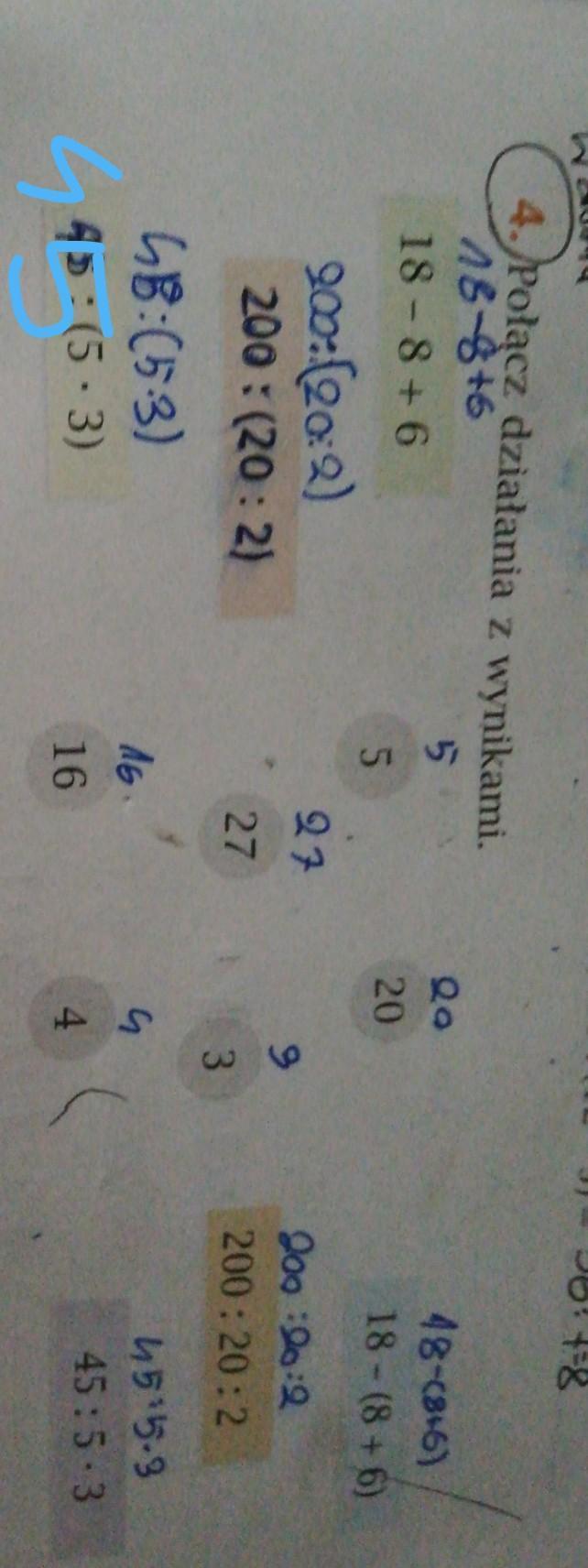
połącz działania z wynikami plss pomużcie ​

question img

Odpowiedzi 1

Odpowiedź:

Szczegółowe wyjaśnienie:

18-8+6=16

200:(20:2)=20

45:(5x3)=3

18-(8+6)=4

200:20:2=5

45:5x3=27

Znasz odpowiedź? Dodaj ją tutaj!

Can't find the answer?

Other related questions that may help you

iloczyn dwóch kolejnych liczb całkowitych patrzystych jest równy kwadratowi mniejszej z nich. Co to za liczby?? iloczyn dwóch kolejnych liczb całkowitych patrzystych jest równy kwadratowi większej z nich. Co to za liczby?? daje najj błagam ​

Odpowiedź i szczegółowe wyjaśnienie:

Dwie kolejne liczby całkowite parzyste to:

2n+2

2n+4

I teraz tworzymy równanie z zadania:

iloczyn dwóch kolejnych liczb całkowitych parzystych jest równy kwadratowi mniejszej z nich.

I rozwiązujemy:

[tex](2n+2)\cdot(2n+4)=(2n+2)^2\\4n^2+8n+4n+8=4n^2+8n+4\\4n^2+12n+8=4n^2+8n+4\\4n^2+12n-4n^2-8n=4-8\\4n=-4\ /:4\\n=-1\\[/tex]

A więc nasze liczby to:

[tex]2n+2 = 2\cdot(-1)+2=-2+2=0\\\\2n+4=2\cdot(-1)+4=-2+4=2[/tex]

Sprawdzamy warunek zadania:

0*2 = 0^2

0=0

L=P

zatem, nasze liczby to: 0 i 2

Połącz nazwy i skróty z właściwymi wyjaśnieniami ich znaczenia. Seelöwe Messerschmitt. • brytyjski myśliwiec odznaczający się szybkością i zwrotnością . niemiecki plan inwazji na Wyspy Brytyjskie brytyjska marynarka wojenna • brytyjskie siły powietrzne RAF. Spitfire • niemiecki samolot będący na wyposażeniu armii III Rzeszy​
question img

Odpowiedź:

Seelöwe→ niemiecki plan inwazji na Wyspy Brytyjskie

Wyjaśnienie:

Pozdrawiam GroZa (;

4. a) W każdym z frazeologizmów wskaż wyraz, który jest jego ośrodkiem. dać komuś wolną rękę. nadużywać czyjejś uprzejmości • trafić z deszczu pod rynnę mieć wilczy apetyt niedaleko pada jablko od jabłoni puszczać perskie oko • walczyć z wiatrakami b) Wyjaśnij znaczenie podanych frazeologizmów.​
question img

Odpowiedź:

Wyjaśnienie:

Dać komuś wolną rękę.

Nadużywać czyjejś uprzejmości.

Trafić z deszczu pod rynnę.

Mieć wilczy apetyt.

Niedaleko pada jabłko od jabłoni.

Puszczać perskie oko.

Walczyć z wiatrakami.

533. Dobierz współczynniki stechiometryczne w podanych równaniach reakcji chemicznych metodą bilansu elektronowego. Wskaż utleniacz i reduktor. d) HNO3 + I2 ->HIO3 + NO + H2O e) MnO2 + HCl - > MnCl2 + Cl2 + H2O​

Witaj :)

Rozwiązanie w załączniku

answer img

Other Matematyka Questions

Zaloguj się z Google

 lub

Zapomniałeś(aś) hasła?

Nie mam jeszcze konta, ale chcę je założyć Zarejestruj się

Wybierz język i region

English

United States

Polski

Polska

Português

Brasil

English

India

English

Philippines

Español

España

Bahasa Indonesia

Indonesia

Türkçe

Türkiye
How much to ban the user?
1 hour 1 day 100 years