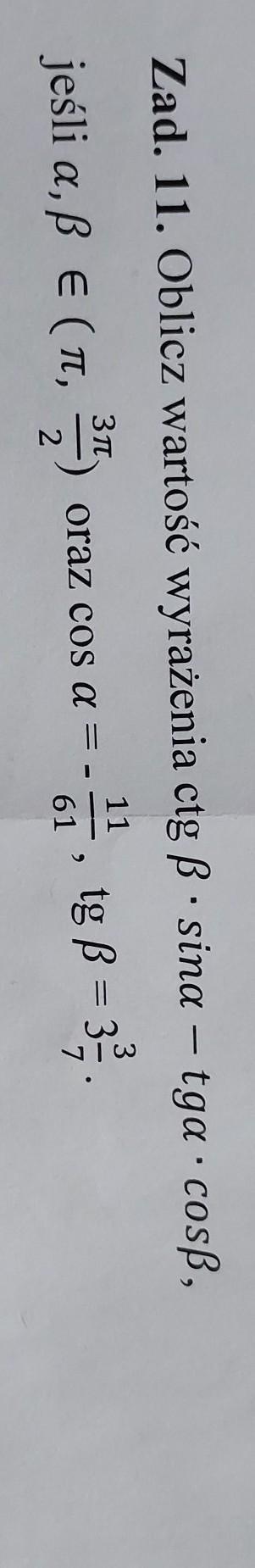Wymień 3 wykonawców i zespoły zajmujące się muzyką na wesoło.

Odpowiedź:

1. obrazki

2. myśli bohaterów

3. krótkie wypowiedzi

4. akcja

Wyjaśnienie:

Łatwiej byłoby gdyby był ten obrazek

Odpowiedź:

Charakterystyczne cechy komiksu to: * duża ilość obrazków, ilustracji, * skąpa ilość tekstu (występuje on w dwóch rodzajach: jako słowa dialogu w „chmurkach” oraz jako komentarz pisany ciągłym tekstem w ramkach lub luźno na stronie), * fabularny charakter, * odcinkowość

Odpowiedź:

[tex]\text{ctg }\beta*\sin\alpha-\text{tg }\alpha*\cos\beta=1\frac{1613}{6710}[/tex]

Szczegółowe wyjaśnienie:

Zauważmy, że kąty [tex]\alpha[/tex] i [tex]\beta[/tex] są z trzeciej ćwiartki, więc mają ujemne sinusy i cosinusy, a dodatnie tangensy i cotangensy.

Policzmy brakujące wartości funkcji trygonometrycznych dla kąta [tex]\alpha[/tex].

[tex]\cos\alpha=-\frac{11}{61}\\\sin^2\alpha+\cos^2\alpha=1\\\sin^2\alpha+(-\frac{11}{61})^2=1\\\sin^2\alpha+\frac{121}{3721}=1\\\sin^2\alpha=1-\frac{121}{3721}\\\sin^2\alpha=\frac{3600}{3721}\\\sin\alpha=\sqrt{\frac{3600}{3721}}\vee \sin\alpha=-\sqrt{\frac{3600}{3721}}\\\underbrace{\sin\alpha=\frac{60}{61}}_{\text{odrzucamy}}\vee \sin\alpha=-\frac{60}{61}\\\sin\alpha=-\frac{60}{61}\\\text{tg }\alpha=\frac{\sin\alpha}{\cos\alpha}\\\text{tg }\alpha=\frac{-\frac{60}{61}}{-\frac{11}{61}}=\frac{60}{11}[/tex]

Policzmy brakujące wartości funkcji trygonometrycznych dla kąta [tex]\beta[/tex].

[tex]\text{tg }\beta=3\frac{3}{7}=\frac{24}{7}\\\text{ctg }\beta=\frac{1}{\text{tg }\beta}=\frac{7}{24}\\\text{tg }\beta=\frac{\sin\beta}{\cos\beta}\\\frac{\sin\beta}{\cos\beta}=\frac{24}{7}\ |*\cos\beta\\\sin\beta=\frac{24}{7}\cos\beta\\\sin^2\beta+\cos^2\beta=1\\(\frac{24}{7}\cos\beta)^2+\cos^2\beta=1\\\frac{576}{49}\cos^2\beta+\cos^2\beta=1\\\frac{576}{49}\cos^2\beta+\frac{49}{49}\cos^2\beta=1\\\frac{625}{49}\cos^2\beta=1\ |*\frac{49}{625}\\\cos^2\beta=\frac{49}{625}[/tex]

[tex]\cos\beta=\sqrt{\frac{49}{625}}\vee\cos\beta=-\sqrt{\frac{49}{625}}\\\underbrace{\cos\beta=\frac{7}{25}}_{\text{odrzucamy}}\vee\cos\beta=-\frac{7}{25}\\\cos\beta=-\frac{7}{25}[/tex]

Policzmy wartość podanego wyrażenia.

[tex]\text{ctg }\beta*\sin\alpha-\text{tg }\alpha*\cos\beta=\frac{7}{24}*(-\frac{60}{61})-\frac{60}{11}*(-\frac{7}{25})=\frac{7}{2}*(-\frac{5}{61})-\frac{12}{11}*(-\frac{7}{5})=\\=-\frac{35}{122}+\frac{84}{55}=-\frac{1925}{6710}+\frac{10248}{6710}=\frac{8323}{6710}=1\frac{1613}{6710}[/tex]

Odpowiedź:

1:

Gaz (para wodna) ------> Ciało stałe (lód) - resublimacja

Ciało stałe (lód) ------> Gaz (para wodna) - sublimacja

Gaz (para wodna) ------> Ciecz (woda) - skraplanie

Ciecz (woda) ------> Gaz (para wodna) - parowanie

Ciecz (woda) ------> Ciało stałe (lód) - krzepnięcie

Ciało stałe (lód) ------> Ciecz (woda) - topnięcie

2:

Ciało stałe ------> Ciecz - topnienie

3:

Ciało stałe ------> Gaz

4:

Gaz ------> Ciało stałe

Mam nadzieje że dobrze i że pomogłam.

Licze na naj.

napięcie wyniesie 150 000V