Co jest żródłem dźwięku w instrumentach strunowych.

Odpowiedź:

Pole koła  P = πr² = πd²/4 = 58π/4 = 14,5π

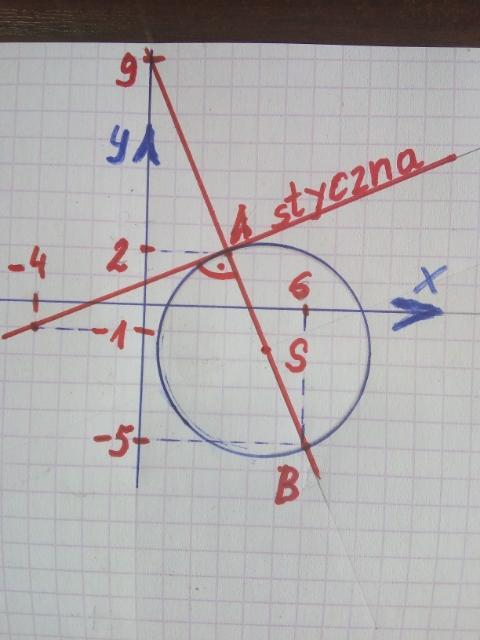
Równanie stycznej do koła w punkcie A:  y = (3/7)x + 5/7

Szczegółowe wyjaśnienie:

(ilustracja graficzna - załącznik)

A(x, y) = A(3, 2) i B(6, -5)

Średnicę koła  d wyznaczymy z tw. Pitagorasa:

d² = (6 - 3)² + (- 5 - 2)² = 9 + 49 = 58    to   |d| = √58

Pole koła  P = πr² = πd²/4 = 58π/4 = 14,5π

Równanie prostej zawierającej średnicę AB,  w postaci kierunkowej

y = mx + n,  (y = ax +b),  gdzie współczynnik kierunkowy (z współrzędnych punktów  A  i  B)   m = tg ∝ = - (-5 - 2)/(6 - 3) = - 7/3

[lub liczymy krateczki na rysunku: (7 krateczek w pionie)/(3 krateczki w poziomie),  " - ",   bo  ∝ ∈(90º, 180º)]      to

równanie prostej AB:   y = (-7/3)x + n   i punkt   A(3, 2)    to

2 = (- 7/3)3 + n   to    n = 9   to    AB:  y= (-7/3)x + 9

Równanie stycznej:   Z warunku prostopadłości dwóch prostych

1 + m1m2 = 0   to   1 + (-7/3)m2 = 0 szukane  m2 = 3/7    to,  jak wyżej,

podstawiamy współrzędne punktu A:,

to: Odpowiedź:

Równanie stycznej do koła w punkcie A:  y = (3/7)x + 5/7

[Jeśli rysunek wykona się dokładnie - to równania prostych i odpowiedzi na inne pytania postawione w zadaniu, można "czytać" wprost z rysunku!]

Odpowiedź:

mam nadzieję że pomogłam

Odpowiedź:

Wyjaśnienie:

wprowadzenie

komedia

dramat

przeznaczenie

O tym, że prawda jest przejawem odwagi mogliśmy się przekonać dzięki następującym utworom literackim:

1. "Zbrodnia i kara" Fiodora Dostojewskiego - główny bohater powieści zataja swoją zbrodnię, jednak męczą go wyrzuty sumienia. Dopiero kiedy ma on szansę być szczery sam ze sobą oraz z Sonią, przechodzi przemianę. Prawda była dla Raskolnikowa bardzo trudna, a stawienie jej czoło świadczyło o jego odwadze.
2. "Antygona" Sofoklesa - Antygona otwarcie przyznaje, że postąpiła wbrew prawom Kreona, mimo że wie, że karą za taką winę jest śmierć. Antygona jest jednak odważna, nie lęka się konsekwencji i nie zamierza kłamać.
3. "W pustyni i w puszczy" Henryka Sienkiewicza - Staś Tarkowski otwarcie mówi o swojej wierze i nie zamierza oddawać czci innym bogom, mimo że to uchroniłoby jego i Nel od przykrych konsekwencji. Wiedząc, ile ryzykuje, Staś decyduje się na szczerość, co jest przejawem jego odwagi.

Prawda to informacja, którą przekazujemy, wierząc, iż jest prawdziwa, czyli że ma swoje pokrycie w rzeczywistości.

Człowiek w swoich badaniach i rozważaniach dąży do poznania tzw. prawdy obiektywnej, która istnieje niezależnie od poglądów jednostki.

#SPJ1