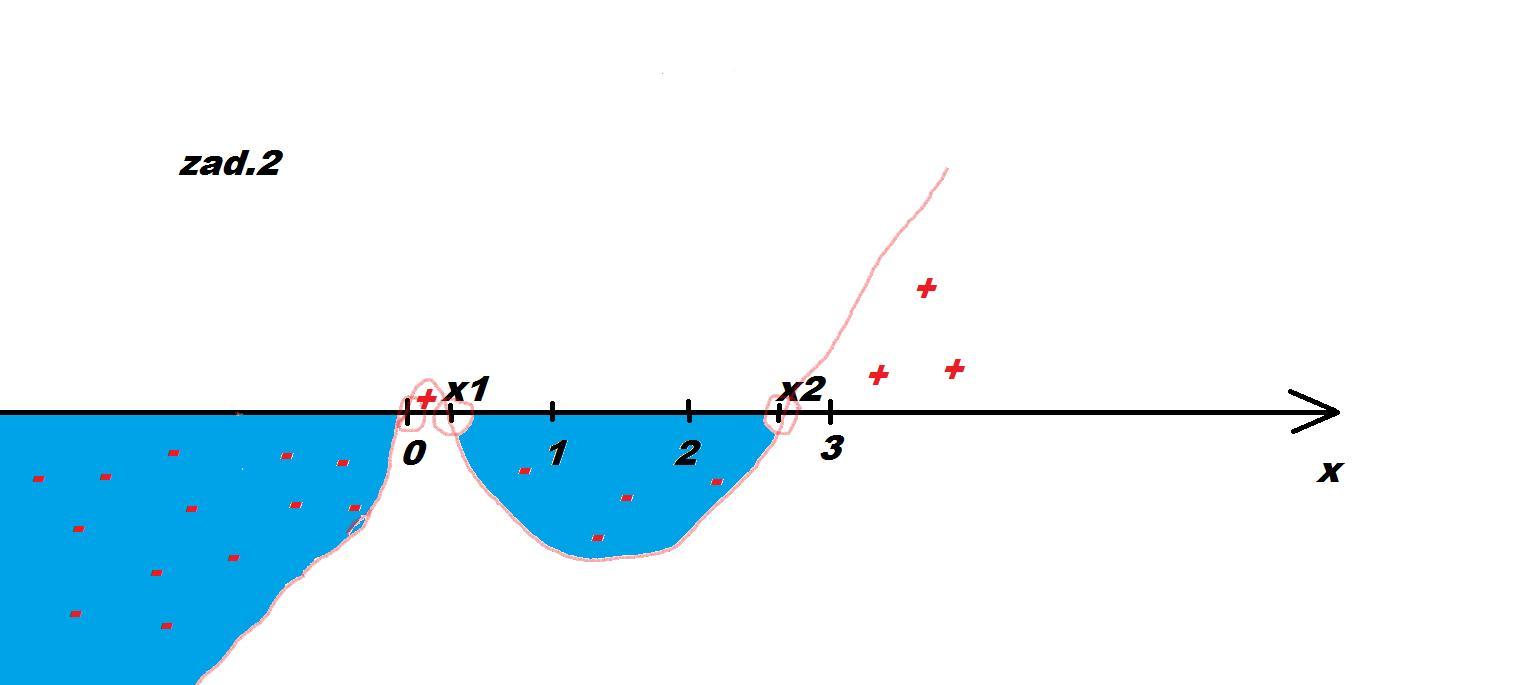
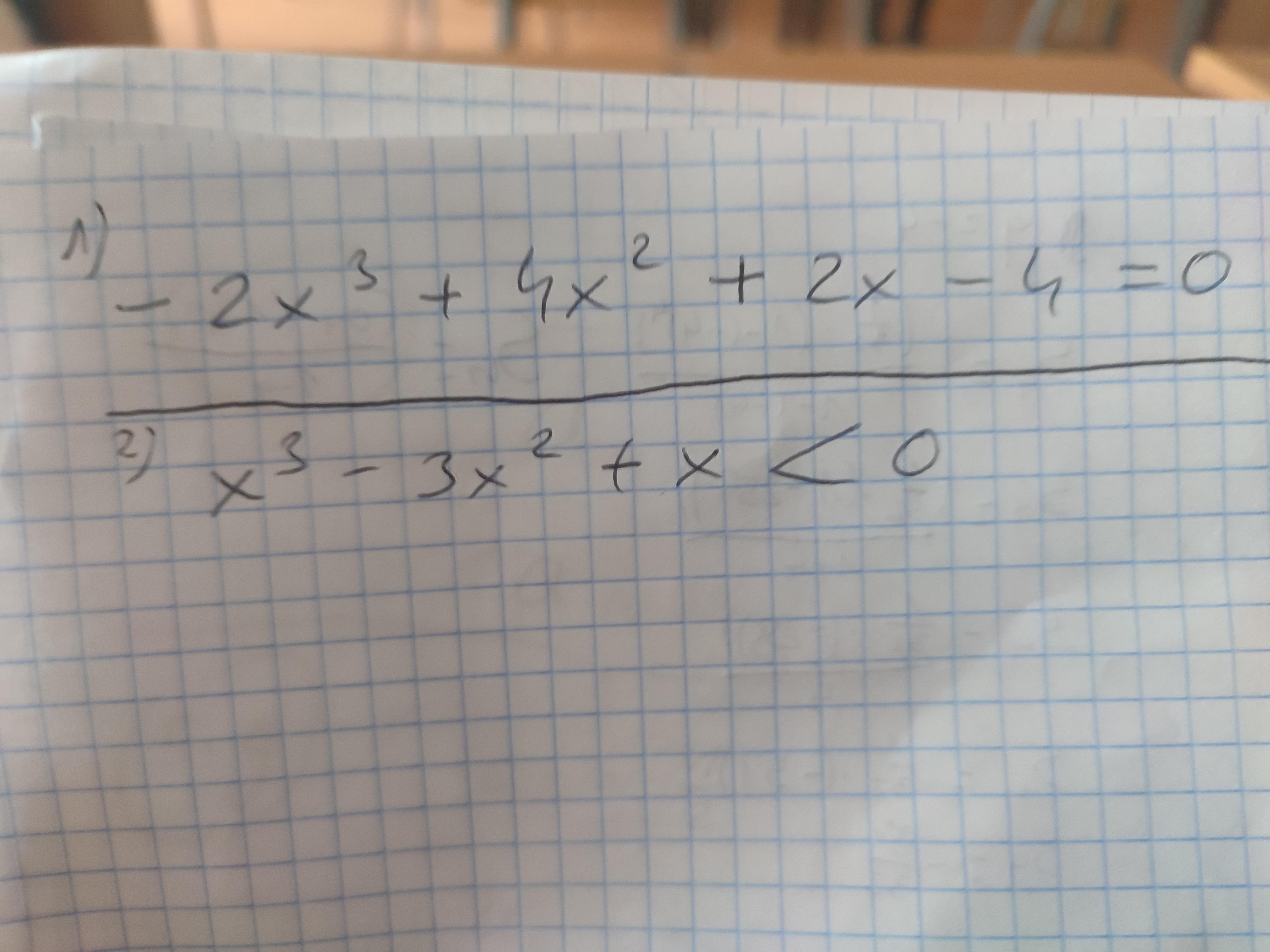Uszereguj kolejno działania podejmowane przy rejestracji działalności gospodarczej: a) wyrobienie pieczątki firmowej b) powiadomienie Państwowej Inspekcji Pracy i Państwowej Inspekcji Sanitarnej c) Zakład Ubezpieczeń społecznych - zgłoszenie do ubezpieczenia d) Urząd Skarbowy - numer NIP e) Sąd Rejonowy - wpis do rejestru przedsiębiorstw f) Wojewódzki Urząd Statystyczny - numer REGON g) założenie rachunku w banku.

Odpowiedź:

[tex]zad.1~~x=-1~~\lor~~x=1~~\lor~~x=2\\\\zad.2~~x\in (-\infty ,0)\cup (\dfrac{3-\sqrt{5} }{2} ,\dfrac{3+\sqrt{5} }{2} )[/tex]

Szczegółowe wyjaśnienie:

[tex]zad.1\\\\-2x^{3} +4x^{2} +2x-4=0\\\\-2x^{2} \cdot (x -2)+2\cdot (x-2)=0\\\\(x-2)\cdot (-2x^{2} +2)=0\\\\(x-2)\cdot 2\cdot (1-x^{2} )=0~~\mid~~\div 2\\\\(x-2)\cdot (1-x^{2} )=0\\\\[/tex]

Korzystam ze wzoru skróconego mnożenia :

[tex]x^{2} -y^{2} =(x-y)\cdot (x+y)[/tex]

[tex]1 -x^{2} =1^{2} -x^{2} =(1-x)\cdot (1+x)\\\\(x-2)\cdot (1-x)\cdot (1+x)=0\\\\x-2=0~~\lor~~1-x=0~~\lor~~1+x=0\\\\x=2~~\lor~~x=1~~\lor~~x=-1[/tex]

Odp:  Rozwiązanie równania : x = -1  ∨  x = 1  ∨  x = 2.

[tex]zad.2\\\\x^{3} -3x^{2} +x < 0\\\\x\cdot ( x^{2} -3x+1) < 0\\\\x=0~~\lor ~~x^{2} -3x+1=0\\\\x^{2} -3x+1=0~~~~\lor~~~~x=0\\\\a=1,~~b=-3,~~c=1\\\\\Delta=b^{2} -4ac\\\\\Delta=(-3)^{2} -4\cdot 1\cdot 1=9-4=5\\\\\sqrt{\Delta} =\sqrt{5} \\\\x_{1} =\dfrac{-b-\sqrt{\Delta} }{2a} ~~\lor~~x_{2} =\dfrac{-b+\sqrt{\Delta} }{2a}\\\\\\(~~x_{1} =\dfrac{3-\sqrt{5} }{2\cdot 1} ~~\lor~~x_{2} =\dfrac{3+\sqrt{5} }{2\cdot 1}~~)~~\land~~\sqrt{5} \approx 2,24\\\\x_{1} \approx 0,38~~\lor~~x_{2} \approx 2,62\\[/tex]

[tex]x=\dfrac{3-\sqrt{5} }{2} ~~\lor~~x=\dfrac{3+\sqrt{5} }{2} ~~\lor~~x=0\\\\\\x^{3} -3x^{2} +x < 0~~\Leftrightarrow~~x\in (-\infty ,0)\cup (\dfrac{3-\sqrt{5} }{2} ,\dfrac{3+\sqrt{5} }{2} )\\\\\\\\Odp:~~x\in (-\infty ,0)\cup (\dfrac{3-\sqrt{5} }{2} ,\dfrac{3+\sqrt{5} }{2} )[/tex]

Odpowiedź:

Ponieważ prędkość jest stała,

oraz

  = 0 i pozioma składowa pchania pracownika Fcosθ (gdzie θ = 32

  ) musi być równa wielkości siły tarcia f

k

  = μ

k

  F.

N

  . Ponadto siły pionowe muszą się znosić, co oznacza

             W

stosowany

  = (8,0N) (0,70m) = 5,6J

co jest rozwiązane, aby znaleźć F = 71N.

(a) Praca wykonana na bloku przez pracownika to, przy użyciu równania. 7-7,

                                  W = Fdcosθ = (71N) (9,2 m) cos32

  = 5,6 × 10

2

  J.

(b) Ponieważ f

k

  = μ

k

  (mg + Fsinθ), znajdujemy ΔE

ten

  = f

k

  d = (60N) (9,2m) = 5,6 × 10

2

  J.

Wyjaśnienie:

Odpowiedź:

Prozdrowotne:

- odpowiednią ilość snu

-Sport

- zdrowe odżywianie

- relax

Ogólnie rzeczy które nas uspokajają i poprawiają nam humor

tyle pomogę ;)

Wyjaśnienie: