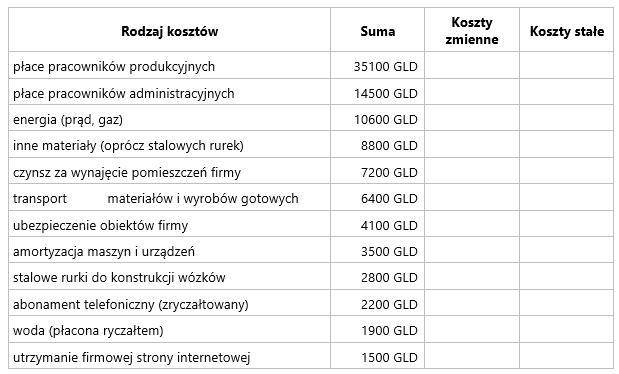
Witam pomoże mi ktoś obliczyć koszta całkowite produkcji firmy? Wasza firma, która produkuje wózki dziecięce, ponosi w ciągu tygodnia następujące koszty (wyrażone w GLD, czyli lokalnej walucie): W ciągu tygodnia produkujecie 170 wózków dziecięcych. 1) Wpierw obliczcie koszt zmienny całkowity oraz koszt stały całkowity waszej tygodniowej produkcji. [Do obliczeń możecie wykorzystać powyższą tabelę.] Wyniki: ………………………………………. 2) Teraz obliczcie, ile wynosi koszt wyprodukowania 1 wózka dziecięcego. Obliczenia: Wyniki: ………………………………………. Z zamówionych badań dowiadujecie się, że funkcja kosztu całkowitego produkcji wózków dziecięcych ma postać: KC = Q3 – 360Q2 + 32960Q, gdzie: KC – koszt całkowity, Q – tygodniowa produkcja wózków w sztukach. 3) Obliczcie, przy jakiej tygodniowej ilości produkcji wózków osiągany jest minimalny koszt całkowity przeciętny. (Wskazówka: przypomnijcie sobie, co się dzieje w zakresie kosztów, gdy koszt całkowity przeciętny osiąga minimum.) Po dokonaniu tych obliczeń ustalcie, czy w waszej firmie osiągnięto minimalny koszt produkcji 1 wózka dziecięcego. Obliczenia:

Odpowiedź:

a= dł. krawedzi podstawy         h= dł. krawedzi bocznej

8a+4h= 24   /:4

2a+h= 6           h= 6-2a

Pc= 2a²+4ah= 2a²+4a*( 6-2a)= 2a²+24a-8a²= -6a²+24a

a>0       h>0             6-2a>0                     -2a<-6                   a<3

D= (0,3)

P(a)=  -6a²+24a   mamy f. kwadratowa o ujemnym współczynniku przy a², ramiona paraboli skierowane będa w dół, czyli wartośc max jest w wierzchołku

p=-b/2a= -24/-12=2                  wiec a= 2             h= 6-2*2=2

najwieksze pole całkowite bedzie miał prostopadłoscian o krawedzi podstawy a=2  i  wysokosc h= 2, czyli bedzie to po prostu szescian

Szczegółowe wyjaśnienie:

[tex]P=6[/tex]

Dane:

[tex]y=x^2-6x+11\\y=-2x+11[/tex]

Szukane:

pole trójkąta, który powstanie z wierzchołka funkcji y=x²-6x+11 oraz punktów przecięcia tej funkcji z funkcją y=-2x+11

Rozwiązanie:

Pierwszym krokiem będzie wyliczenie współrzędnych wierzchołka funkcji y=x²-6x+11.

[tex]y=x^2-6x+11\\W_1=(p,q)\\p=-\frac{b}{2a} \\p=-\frac{-6}{2}\\p=3\\q=-\frac{b^2-4ac}{4a}\\ q=-\frac{(-6)^2-4*1*11}{4}\\q=-\frac{36-44}{4}\\q=2\\W_1=(3,2)[/tex]

Teraz wyliczony wierzchołek paraboli oznaczymy sobie jako punkt C.

[tex]W_1=C\\C=(3,2)[/tex]

Następnie wyliczymy punkty przecięcia funkcji y=x²-6x+11 z funkcją y=-2x+11. Aby to zrobić, należy przyrównać do siebie obie te funkcje, przez co wyjdzie nam współrzędna x, a następnie trzeba podstawić x do jednego ze wzorów funkcji i wyjdzie nam współrzędna punktu y.

[tex]y=x^2-6x+11\\y=-2x+11\\y=y\\x^2-6x+11=-2x+11\\x^2-6x+11+2x-11=0\\x^2-4x=0\\x(x-4)=0\\x_1=0\\x_2=x-4=0\\x_2=4[/tex]

, zatem:

[tex]y_1=-2x_1+11\\y_1=11\\y_2=-2x_2+11\\y_2=-2*4+11\\y_2=3[/tex]

Teraz poszczególne punkty przecięcia funkcji oznaczymy sobie jako A oraz B.

[tex]A=(x_1,y_1)\\A=(0,11)\\B=(x_2,y_2)\\B=(4,3)[/tex]

Ostatnim krokiem będzie wyliczenie pola trójkąta korzystając z poniższego wzoru.

[tex]P=\frac{1}{2} |(x_B-x_A)(y_C-y_A)-(y_B-y_A)(x_C-x_A)|\\P=\frac{1}{2} |(4-0)(2-11)-(3-11)(3-0)|\\P=\frac{1}{2} |4*(-9)-(-8)*3|\\P=\frac{1}{2} |-36-(-24)|\\P=\frac{1}{2} |-36+24|\\P=\frac{1}{2}|-12|\\P=\frac{1}{2}*12\\P=6[/tex]

Cl2

ΔE=3,0-3,0=0                kowalencyjne niespolaryzowane

HF

ΔE=4,0-2,1=1,9              kowalencyjne spolaryzowane

CO2

ΔE=3,5-2,5=1,0             kowalencyjne spolaryzowane

CaO

ΔE=3,5-1,0=2,5             jonowe

PH3

ΔE=2,1-2,1=0                 kowalencyjne niespolaryzowane

HBr

ΔE=2,8-2,1=0,7             kowalencyjne spolaryzowane

Odpowiedź:

F =2,7 · 10^¹² [N]

Wyjaśnienie:

Obliczenia w załączniku.