Plsss zrób ktoś dam follow i naj!!do 15 mam to wiec prosze❤❤❤​

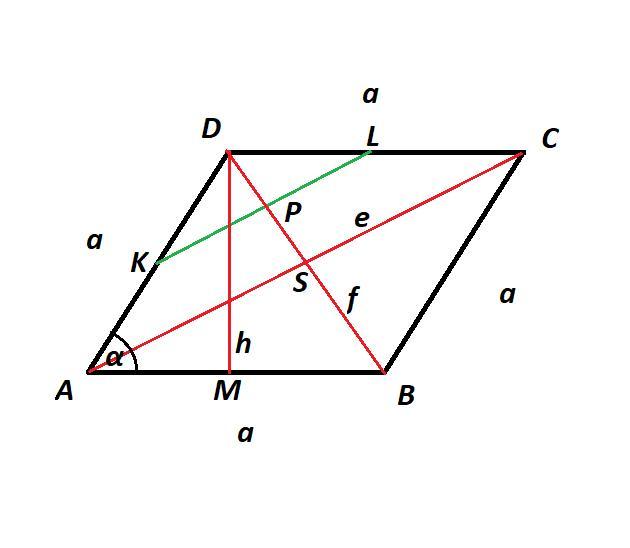
Trójkąty [tex]DKL[/tex] i [tex]ACD[/tex] są do siebie podobne. Dlatego [tex]\frac{|KL|}{|AC|} = \frac{|DK|}{|AD|}[/tex].

Jak wynika z treści zadania, [tex]|DK| = \frac{|AD|}{2}[/tex].

A zatem:

[tex]\frac{|KL|}{|AC|} = \frac{\frac{|AD|}{2} }{|AD|} = \frac{|AD|}{2} \cdot \frac{1}{|AD|} = \frac{1}{2}[/tex]

Odcinek [tex]AC[/tex], będący przekątną [tex]e[/tex] rombu, jest [tex]2[/tex] razy dłuższy niż odcinek [tex]KL[/tex].

Obliczam [tex]e[/tex]:

[tex]e = 2 \cdot |KL| = 2 \cdot 2,4\ \textup{dm} = 4,8\ \textup{dm}[/tex]

Teraz mogę łatwo obliczyć długość przekątnej [tex]f[/tex] ze wzoru [tex]P = \frac{ef}{2}[/tex]:

[tex]ef = 2P\\f = \frac{2P}{e} = \frac{2\ \cdot\ 4,8\ \textup{dm}^2}{4,8\ \textup{dm}} = 2\ \textup{dm}[/tex]

Trójkąt [tex]BCS[/tex] jest trójkątem prostokątnym, w którym długości przyprostokątnych to [tex]\frac{e}{2} = \frac{4,8\ \textup{dm}}{2} = 2,4\ \textup{dm}[/tex] i [tex]\frac{f}{2} = \frac{2\ \textup{dm}}{2} = 1\ \textup{dm}[/tex]. Mogę zatem obliczyć długość boku rombu, wykorzystując twierdzenie Pitagorasa:

[tex]a = \sqrt{\left( 2,4\ \textup{dm} \right) ^2 + \left( 1\ \textup{dm} \right) ^2} = \sqrt{5,76\ \textup{dm}^2 + 1\ \textup{dm}^2} = \sqrt{6,76\ \textup{dm}^2} = 2,6\ \textup{dm}[/tex]

Teraz mogę obliczyć obwód [tex]L[/tex]:

[tex]L = 4a = 4 \cdot 2,6\ \textup{dm} = 10,4\ \textup{dm}[/tex]

Wykorzystuję wzór na pole powierzchni [tex]P = ah[/tex], żeby obliczyć wysokość:

[tex]h = \frac{P}{a} = \frac{4,8\ \textup{dm}^2}{2,6\ \textup{dm}} \approx 1,85\ \textup{dm}[/tex]

Pole trójkąta [tex]DKL[/tex] jest równe [tex]\frac{|KL| \cdot |DP|}{2}[/tex]. Długość odcinka [tex]KL[/tex] jest dana w treści zadania, natomiast długość odcinka [tex]DP[/tex] jest dwa razy krótsza niż długość odcinka [tex]DS[/tex] (co wynika z wcześniej ustalonej skali podobieństwa trójkątów), ten zaś jest połową przekątnej [tex]f[/tex].

[tex]P = \frac{|KL| \cdot \frac{\frac{f}{2} }{2} }{2} = \frac{|KL| \cdot f}{8} = \frac{2,4\ \textup{dm}\ \cdot\ 2\ \textup{dm}}{8} = 0,6\ \textup{dm}^2[/tex]

Odpowiedź

Długości przekątnych rombu to [tex]4,8\ \textup{dm}[/tex] i [tex]2\ \textup{dm}[/tex]. Obwód rombu jest równy [tex]10,4\ \textup{dm}[/tex]. Wysokość rombu wynosi w przybliżeniu [tex]1,85\ \textup{dm}[/tex]. Pole trójkąta wyciętego z rombu przez dany odcinek to [tex]0,6\ \textup{dm}^2[/tex].

Odpowiedź:

w zalaczniku odpowiedź

Wyjaśnienie:

Odpowiedź:

dach- piach

stach- szach

mech- wdech

puch - duch

7.

ruch

węch

paluch

druh

strach

duch

Proszę bardzo :)

Zadanie 1.

dach - strach

stach - piach

mech - grzech

puch - brzuch

Zadanie 2.

ruch

węch

paluch

druh

strach

duch

Odpowiedź:

Wyjaśnienie:

a) 36km/h=36*1000 m/3600 s=36/3,6=10 m/s

b) 20cm/s=20 *1/100m*1 s=0,2 m/s

c) 54km/h=54*1000 m/3600 s=54/3,6=16 m/s

_______________________

a) 5m/s=5 *1/1000 km :1/3600 s=5/1000*3600=5*3,6=18 km/h

b) 20 cm/s=20*1/100000 km: 1/3600 h=20/100000*3600=72000/100000=0,72 km/h

c) 0,5 m/s=​0,5*1/1000 km:: 1/3600 h=0,5/1000*3600=1,8 km/h