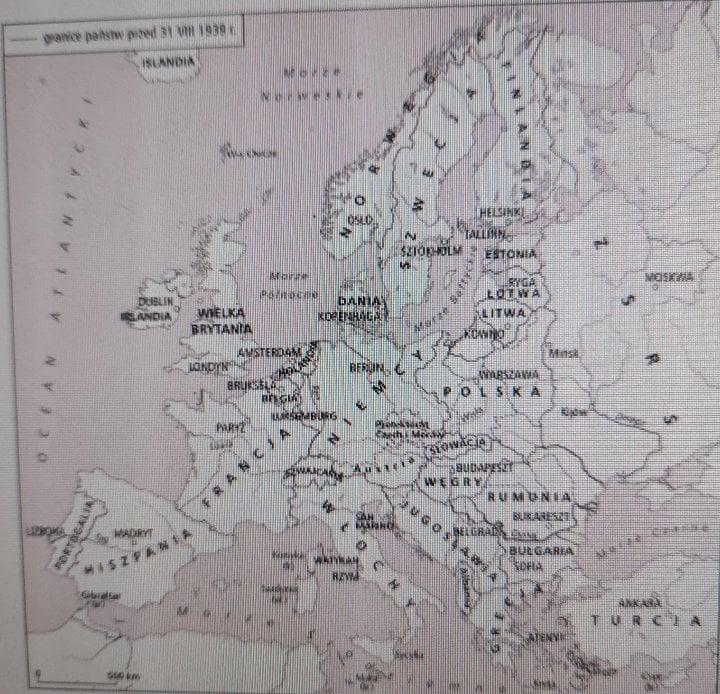
Proszę o Pomoc!b) Zamaluj koloremniebieskim terenyokupowane przezpaństwa osi wlistopadzie 1939 r.

question img

Odpowiedzi 1

Cześć!

Zamaluj Czechosłowację oraz Polskę.

Pozdrawiam

Znasz odpowiedź? Dodaj ją tutaj!

Can't find the answer?

Other related questions that may help you

21. Dany jest układ równań z niewiadomymi x i y c. Wykaż, że jeśli ten układ jest nieoznaczony, to 11a+3b+12=0układ:(2a-1)x-3y=4ax+4y=b​

Odpowiedź i szczegółowe wyjaśnienie:

Układ nieoznaczony oznacza, że ma nieskończenie wiele rozwiązań. A tym samym proste określone w układzie pokrywają się tzn. mają te same współczynniki w funkcji.

Zatem:

[tex]\left \{ {{(2a-1)x-3y=4} \atop {ax+4y=b}} \right. \\\\-3y=-(2a-1)x+4\\4y=-ax+b\\\\y=\dfrac{2a-1}{3}x-\dfrac43\\\\y=\dfrac{-a}{4}x+\dfrac{b}{4}[/tex]

Mamy równania tych funkcji w postaci kierunkowej. Aby one były równoległe odpowiednie współczynniki muszą być sobie równe. Zatem:

[tex]\dfrac{2a-1}{3}=\dfrac{-a}{4}\\\\-3a=4(2a-1)\\\\-3a=8a-4\\\\8a+3a-4=0\\\\11a-4=0[/tex]

[tex]\dfrac{b}{4}=-\dfrac43\\\\-3b=16\\-3b-16=0[/tex]

W związku z tym, że mamy dwa równania:

11a-4=0 oraz -3b-16=0 możemy je do siebie przyrównać i otrzymujemy:

[tex]11a-4=0;\ -3b-16=0\\\\11a-4=-3b-16\\\\11a-4+3b+16=0\\\\11a+3b+12=0[/tex]

Co należało wykazać :)

Średnia arytmetyczna czterech liczb jest równa 8. Jaką liczbę trzeba do nich dopisać, aby średnia arytmetyczna wszystkich pięciu liczb była równa 10? Zapisz obliczenia. Daje naj!!!

Odpowiedź: 18

Szczegółowe wyjaśnienie:

(a+b+c+d)/4 =8

a+b+c+d= 32

chcemy zeby średnia równa była 10

czyli

5*10=50

suma 5 liczb musi byc równa 50

50-32=18

sprawdzenie

(32+18)/5

50/5

10

Odpowiedź:

[tex]\frac{a+b+c+d}{4} =8[/tex]

a + b + c + d = 4 * 8

a + b + c + d = 32

x --> piąta liczba

[tex]\frac{a+b+c+d+x}{5} =10[/tex]  

[tex]\frac{32+x}{5} =10[/tex]

32 + x = 10 * 5

32 + x = 50

x = 50 - 32

x = 18

Odp. Do liczb trzeba dopisać liczbę 18, aby średnia arytmetyczna wszystkich pięciu wyniosła 10.

2. Samochód przejechał pierwsze 150 km podróży w 2 godziny, a następne 50 km w pół godziny. Jaką łączną odległość przeby i w jakim czasie? Z jaką średnią prędkością pokonał cały dystans?nie czeba się śpieszyć ale dam naj ​

Łączna odległość: s= 150 km+50 km = 200 km

Łączny czas: t= 2 h+0,5 h=2,5 h

Średnia prędkość:

v=s/t

v= 200km/2,5h

v=80 km/h

właściwości pierwiastków chemicznych zmieniają się w sposób okresowych poniżej uporządkowano pierwiastki chemiczne według pewnych zasad ​
question img

Odpowiedź:

A i E

Wyjaśnienie:

W okresie charakter zasadowy  i metaliczność pierwiastków rosną od prawej do lewej.

Other Historia Questions

Zaloguj się z Google

 lub

Zapomniałeś(aś) hasła?

Nie mam jeszcze konta, ale chcę je założyć Zarejestruj się

Wybierz język i region

English

United States

Polski

Polska

Português

Brasil

English

India

English

Philippines

Español

España

Bahasa Indonesia

Indonesia

Türkçe

Türkiye
How much to ban the user?
1 hour 1 day 100 years