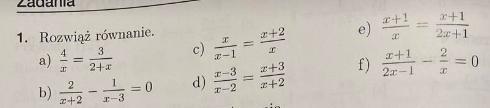Odpowiedź:
Szczegółowe wyjaśnienie:
1.
a)
4/x = 3/(2 + x)
Przy równaniach, nierównościach czy działaniach na wyrażeniach, zawsze zaczynamy od ustalenia Dziedziny funkcji: Df:
W matematyce nie istnieje takie działanie, jak dzielenie przez 0, a w zapisanych tu ułamkach kreska ułamkowa zastępuje znak dzielenia.
Dlatego w dziedzinie funkcji musimy wykluczyć wartość 0 z mianownika.
Wstępnie zapiszemy tak:
x ≠ 0 i 2 + x ≠ 0 to x ≠ 0 i x ≠ - 2
to Dziedzina funkcji: Df: x ∈ R \ {-2, 0}
[Przeczytamy teraz dziedzinę funkcji: x należy do zbioru liczb rzeczywistych, za wyjątkiem zboru dwuelementowego: {- 2, 0}
Druga forma tej regułki: x należy do zbioru liczb rzeczywistych minus zbiór dwuelementowy: {- 2, 0}, (znak \ oznacza odejmowanie zbiorów, różnicę zbiorów - ten znak mamy na klawiaturze.)]
Jeżeli w rozwiązaniu końcowym otrzymamy liczbę, która została wykluczona w Dziedzinie - to takie rozwiązanie nie jest rozwiązaniem tego równania.
Rozwiązujemy równanie: 4/x = 3/(2 + x)
Najpierw mnożymy obie strony równania przez wspólny mianownik, by pozbyć się ułamków: 4/x = 3/(2 + x) /*x(2 + x) to
4(2 + x) = 3x to 8 + 4x = 3x to 4x - 3x = - 8 to x = - 8 _____________________________________ Sprawdzenie
Podstawiamy nasze rozwiązanie do równania wyjściowego - które nie było jeszcze przekształcane:
Lewa strona równania: L = 4/(-8) = - 1/2, P = 3/(2 - 8) = 3/(-6) = - 1/2
to L = P, co należało sprawdzić.
Dopiero teraz możemy dać odpowiedź:
Rozwiązaniem tego równania jest liczba x = - 8
[jeśli coś jest niezrozumiale z przedstawionego rozwiązania, proszę
śmiało pytać w komentarzach, nigdy nie odmawiałem dodatkowych
wyjaśnień.
b)
2/(x + 2) - 1/(x - 3) = 0
Teraz możemy opierać się na bardziej szczegółowo przedstawionym
toku rozwiązywania z przykładu a) - wszystkie przykłady są bardzo podobne.
W Dziedzinie funkcji musimy wykluczyć wartość 0 z mianownika obu
ułamków, to:
Wstępny zapis:
x + 2 ≠ 0 i x - 3 ≠ 0 to x ≠ - 2 i x ≠ 3, to
Dziedzina funkcji: Df: x ∈ R \ {-2, 3}
Rozwiązujemy równanie 2/(x + 2) - 1/(x - 3) /*(x + 2)(x - 3) to
2(x - 3) - 1(x + 2) = 0 to 2x - 6 - x - 2 = 0 to x - 8 = 0 to x = 8
_____________________________________ Sprawdzenie
Podstawiamy nasze rozwiązanie do równania wyjściowego - które nie było jeszcze przekształcane:
Lewa strona równania: L = 2/(8 + 2) - 1(8 - 3) = 2/10 - 1/5 = 1/5 - 1/5 = 0
P = 0 to L = P, co należało sprawdzić.
[Gdyby nam wyszło, że L ≠ P, wtedy musimy szukać błędu] _________________________________________
to: Odpowiedź:
Rozwiązaniem tego równania jest liczba x = 8.
c)
x/(x - 1) = (x + 2)/x
W Dziedzinie funkcji musimy wykluczyć wartość 0 z mianownika obu
ułamków, to:
Wstępny zapis: x - 1 ≠ 0 i x ≠ 0 to x ≠ 1 i x ≠ 0, to
Dziedzina funkcji: Df: x ∈ R \ {0, 1}
Rozwiązujemy równanie x/(x - 1) = (x + 2)/x /*x(x - 1) to
x² = (x + 2)(x - 1) to x² = x² + 2x - x - 2 to x² = x² + x - 2 to
x² - x² - x = - 2 to [ x² - x² = 0] to - x = - 2 /*(-1) to x = 2
_____________________________________ Sprawdzenie:
Podstawiamy nasze rozwiązanie do równania wyjściowego - które nie było jeszcze przekształcane:
Lewa strona równania: L = 2/(2 - 1) = 2/1 = 2 P = (2 + 2)/2 = 4/2 = 2
to L = P, co należało sprawdzić.
[Gdyby nam wyszło, że L ≠ P, wtedy musimy szukać błędu] _________________________________________
to: Odpowiedź:
Rozwiązaniem tego równania jest liczba x = 2.