Co to jest solidaryzm społeczny.

Krzyż, który umieszczamy na grobach przypomina nam że wierzymy w zmartwychwstanie.

Krzyż to znak rozpoznawczy chrześcijan. Katolicy i wyznawcy obrządków wschodnich otaczają go nabożną czcią. Protestanci uznają go za swój symbol, ale odrzucają jego kult, gdyż był narzędziem zbrodni.

Dla większości chrześcijan krzyż jest symbolem męki i śmierci Jezusa Chrystusa, ale też zmartwychwstania - zwycięstwa nad grzechem i śmiercią. Bez krzyża nie byłoby też zbawienia.

W związku z tym, współcześni chrześcijanie umieszczają krzyż na grobach, by pokazać, że wierzą w zmartwychwstanie, a śmierć nie jest końcem.

#SPJ4

Odpowiedź:

Dyfrakcja to zjawisko fizyczne zmiany kierunku rozchodzenia się fali na krawędziach przeszkód oraz w ich pobliżu. Interferencja to zjawisko nakładania się fal prowadzące do zwiększania lub zmniejszania amplitudy fali wypadkowej.

Odpowiedź:

A, D

Wyjaśnienie:

jeśli ci pomogłam to się części

Równanie [tex]|5-2x|=\frac{3p-2}2[/tex] ma dwa rozwiązania przeciwnych znaków dla [tex]p\in(4,+\infty)[/tex].

W równaniach występuje pewna zmienna równania, czyli niewiadoma, względem której równanie to rozwiązujemy, czyli wyznaczamy jej wartość. Najczęściej spotykanym oznaczeniem niewiadomej w równaniu jest litera x.

W równaniu z parametrem pojawia się dodatkowa litera, czyli parametr. Zastępuje on pewną liczbę. W zależności od równania wartość parametru może wpływać na ilość rozwiązań równania.

Mamy równanie [tex]|5-2x|=\frac{3p-2}2[/tex], [tex]p\in\mathbb{R}[/tex]. Przekształcimy je tak, aby po prawej stronie dostać sam parametr.

[tex]|5-2x|=\frac{3p-2}2/*2\\2|5-2x|=3p-2/+2\\2|5-2x|+2=3p/:3\\\frac23|5-2x|+\frac23=p[/tex]

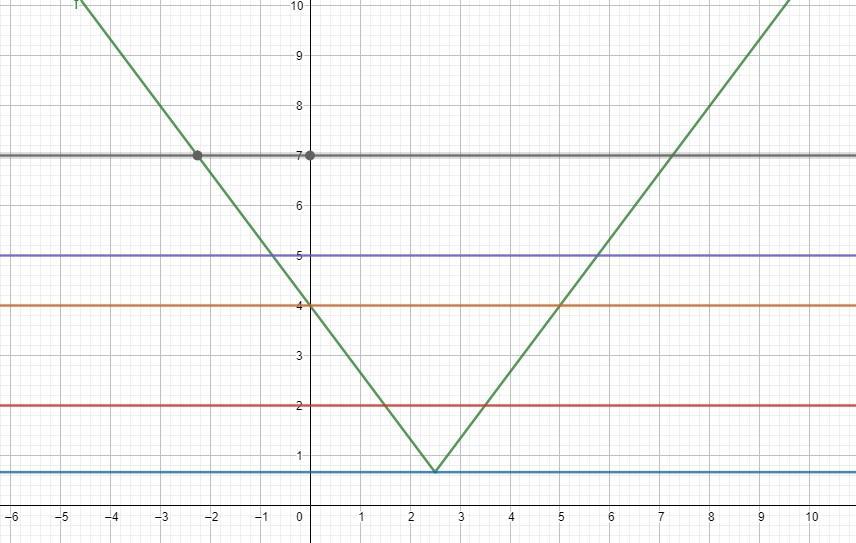
Potraktujmy lewą stronę równania jako funkcję zmiennej x, czyli [tex]f(x)=\frac23|5-2x|+\frac23[/tex]. Wykres jej mamy w załączniku.

Wartości parametru p (które są jednocześnie wartościami naszej funkcji) to linie poziome zaznaczone na wykresie. Dla [tex]p=\frac23[/tex] mamy jedno rozwiązanie równania. Dla [tex]p\in(\frac23,4)[/tex] mamy dwa rozwiązania dodatnie. Dla [tex]p=4[/tex] mamy jedno rozwiązanie dodatnie, drugie równe 0. Dla [tex]p\in(4,+\infty)[/tex] równanie ma dwa rozwiązania różnych znaków.

Dla [tex]p\in(-\infty,\frac23)[/tex] równanie nie ma rozwiązań.

Zatem dla [tex]p\in(4,+\infty)[/tex] równanie [tex]|5-2x|=\frac{3p-2}2[/tex] ma dwa rozwiązania różnych znaków.