Rozwiąże mi ktoś te pytanie plis bardzo proste Daje naj

f(x) = 2(x-1)(ax+1) ; x ∈ R

a) a = 3

f(x) = 2(x-1)(3x+1)

x₀ = 1 V x₀ = -1/3

b)

-4 = 2(4-1)(4a+1)

-4 = 6(4a+1)

-4 = 24a + 6

-10 = 24a

a = -10/24

Odpowiedź:

a) (2x+1)² + (x-3)² < 10

4x²+4x+1+x²-6x+9-10 < 10

4x²+x²+4x-6x+10-10 < 0

5x²-2x < 0

x(5x-2) = 0

x ∈(0; 2/5)

b) 3x-(1-x)² > (x-2)(x+2)

3x-(1-2x+x²) > x²-4

3x -1+2x-x²-x²+4 > 0

-2x²+5x+3 > 3

2x²-5x-3 = 0

x ∈(-1/2,3)

c) (x-3)²-7 < (2x - 1)²

x²-6x+9-7 < 4x²-4x+1

x²-6x+2-4x²+4x-1 < 0

-3x²-2x+1 < 0

x ∈(-∞, -1) U (1/3, + ∞)

Mam nadzieję, że pomogłam :) Liczę na naj, zajęło mi to trochę czasu <3

Odpowiedź:

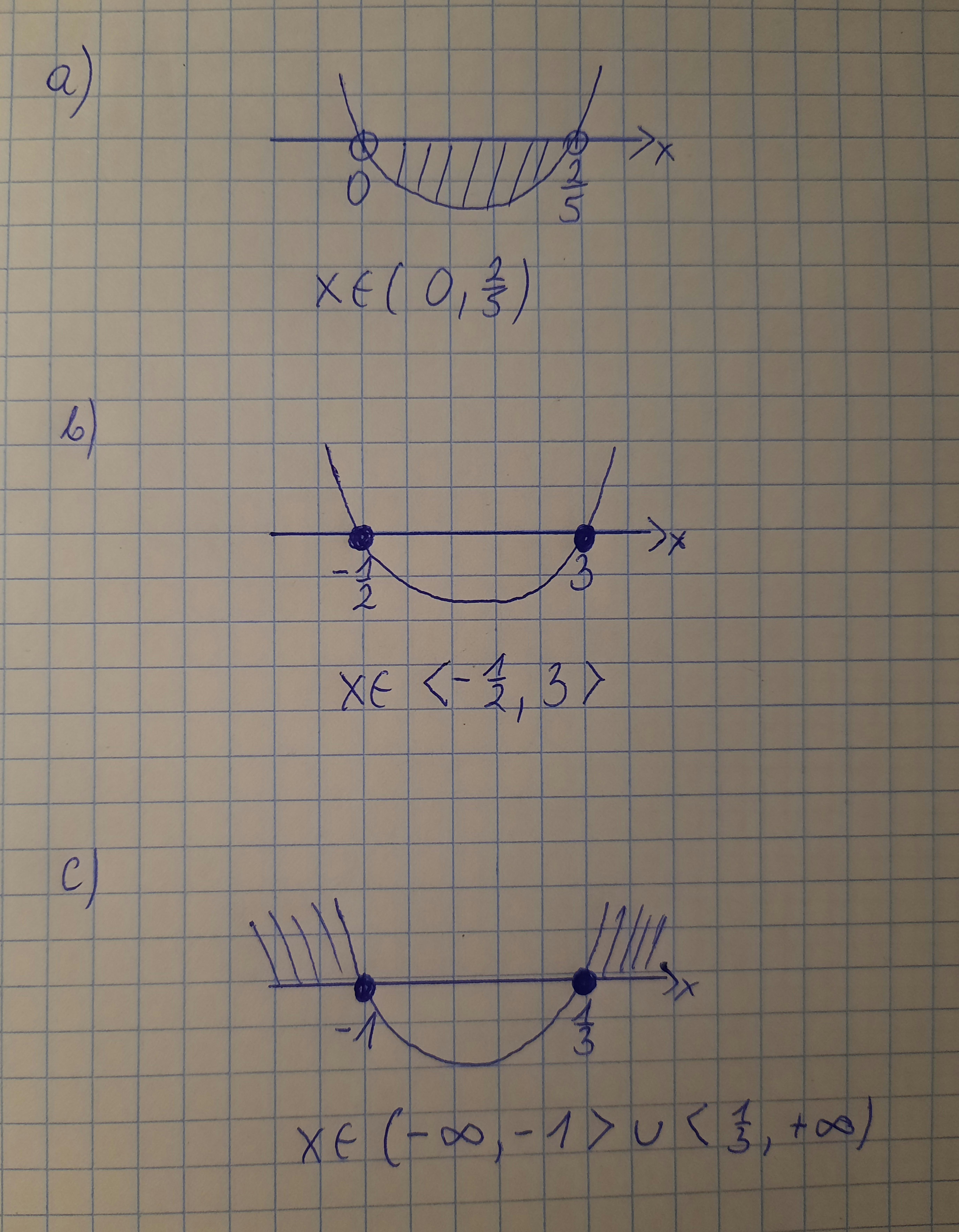
[tex]a)\\\\(2x+1)^2+(x-3)^2 < 10\\\\4x^2+4x+1+(x^2-6x+9) < 10\\\\4x^2+4x+1+x^2-6x+9 < 10\\\\5x^2-2x+10-10 < 0\\\\5x^2-2x < 0\\\\a=5\ \ ,\ \ b=-2\ \ ,\ \ c=0\\\\\Delta=b^2-4ac\\\\\Delta=(-2)^2-4\cdot5\cdot0=4-0=4\\\\\sqrt{\Delta}=\sqrt{4}=2\\\\x_{1}=\frac{-b-\sqrt{\Delta}}{2a}=\frac{-(-2)-2}{2\cdot5}=\frac{2-2}{10}=\frac{0}{10}=0\\\\x_{2}=\frac{-b+\sqrt{\Delta}}{2a}=\frac{-(-2)+2}{2\cdot5}=\frac{2+2}{10}=\frac{4}{10}=\frac{2}{5}[/tex]

[tex]b)\\\\3x-(1-x)^2\geq (x-2)(x+2)\\\\3x-(1-2x+x^2)\geq x^2-4\\\\3x-1+2x-x^2\geq x^2-4\\\\5x-1-x^2-x^2+4\geq 0\\\\-2x^2+5x+3\geq 0\ \ /\cdot(-1)\\\\2x^2-5x-3\leq 0\\\\a=2\ \ ,\ \ b=-5\ \ ,\ \ c=-3\\\\\Delta=b^2-4ac\\\\\Delta=(-5)^2-4\cdot2\cdot(-3)=25+24=49\\\\\sqrt{\Delta}=\sqrt{49}=7\\\\x_{1}=\frac{-b-\sqrt{\Delta}}{2a}=\frac{-(-5)-7}{2\cdot2}=\frac{5-7}{4}=\frac{-2}{4}=-\frac{1}{2}\\\\x_{2}=\frac{-b+\sqrt{\Delta}}{2a}=\frac{-(-5)+7}{2\cdot2}=\frac{5+7}{4}=\frac{12}{4}=3[/tex]

[tex]c)\\\\(x-3)^2-7\leq (2x-1)^2\\\\x^2-6x+9-7\leq4x^2-4x+1\\\\x^2-6x+2-4x^2+4x-1\leq 0\\\\-3x^2-2x+1\leq 0\ \ /\cdot(-1)\\\\3x^2+2x-1\geq 0\\\\a=3\ \ ,\ \ b=2\ \ ,\ \ c=-1\\\\\Delta=b^2-4ac\\\\\Delta=2^2-4\cdot3\cdot(-1)=4+12=16\\\\\sqrt{\Delta}=\sqrt{16}=4\\\\x_{1}=\frac{-b-\sqrt{\Delta}}{2a}=\frac{-2-4}{2\cdot3}=\frac{-6}{6}=-1\\\\x_{2}=\frac{-b+\sqrt{\Delta}}{2a}=\frac{-2+4}{2\cdot3}=\frac{2}{6}=\frac{1}{3}[/tex]

[tex]Zastosowane\ \ wzory\\\\(a+b)^2=a^2+2ab+b^2\\\\(a-b)^2=a^2-2ab+b^2\\\\(a-b)(a+b)=a^2-b^2[/tex]

Jeśli mnożymy lub dzielimy nierówność przez liczbę ujemną to zmieniamy znak nierówności na przeciwny.

f(x) = x

g(x) = -x + 4

f(x) ≤ g(x)

x ≤ -x + 4

2x ≤ 4

x ≤ 2

x ∈ (-∞;2>

Odpowiedź:

42. C

43. B

44. B

45. D

46. D

47. A

48. D

49. B

50. C

Wyjaśnienie:

Liczę na NAJ