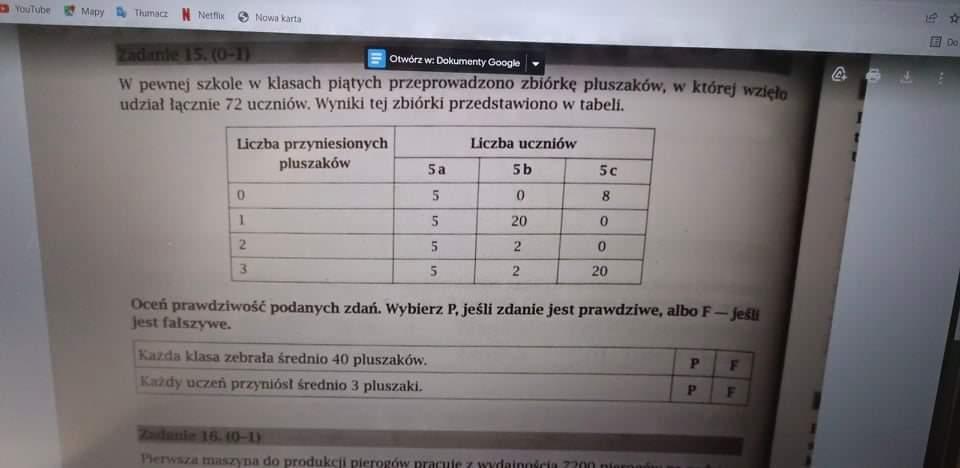
W pewnej szkole w klasach piątych przeprowadzono zbiórkę pluszaków w której wzięło udział łącznie 72 uczniów. Wynik tej zbiórki przedstawiono w tabeli. proszę o pomoc

Odpowiedź:

1 Edyty/Koryntu

2Olimpie

3Nektar

4Ambrozje

5Tanatos

6Pogrzebu

7Hermes

8Głaz

Wyjaśnienie:

Luczę na naj

Odpowiedź:

A. Urbanizacja

B. Miast

C. Złóż surowcow

Odpowiedź:

A. Urbanizacją

B. Krakowa

C. złóż surowców naturalnych

Wyjaśnienie:

Odpowiedź:

To co zakreślone Zad 1

Zad 2

W pierwszej rubryce tabelki wpisz :

Obraz Stalina przedstawiony przez Bieruta ma charakter wiernopoddańczy. Bierut był namiestnikiem Stalina w Polsce, który wypełniał jego derektywy.

W drugiej rubryce napisz:

Stalin był dyktatorem miał krew na rękach kilkudziesięciu milionów ludzi , Rosjanie traktowali go jak bohatera jego pogrzeb był był przykładem kultu przez obywateli który współcześnie jest wyrazem zniewolenia umysłu i wielkiego strachu. Stalin był ludobójca stosował niewyobrażalny terror, był odpowiedzialny za zbrojną agresję na Polskę w 1939 r. Jego rządy pochłonęły miliony ofiar.

Zabierasz się do tego od złej strony.

Kryterium Leibniza:

Jeżeli ciąg [tex](a_n)[/tex] jest malejący, nieujemny i [tex]\lim_{n \to \infty} a_n =0[/tex], to szereg naprzemienny [tex]\Sigma_{n=1}^\infty(-1)^na_n[/tex] jest zbieżny.

Musimy wydobyć z Twojego przykładu postać ciągu  [tex](a_n)[/tex].

[tex]\Sigma_{n=1}^\infty\frac{(-1)^{n+1}}{n}=\Sigma_{n=1}^\infty\frac{(-1)^n*(-1)}{n}=\Sigma_{n=1}^\infty(-1)^n*(-\frac{1}{n})[/tex]

Porównując z szeregiem w kryterium Leibniza, otrzymujemy, że [tex]a_n=-\frac{1}{n}[/tex].

Musimy teraz sprawdzić, czy ten ciąg spełnia warunki kryterium.

Niestety nie spełnia warunku o nieujemności, ale w tym przypadku można to jeszcze uratować z faktu, że jeśli szereg jest zbieżny, to szereg o wyrazach przeciwnych też jest zbieżny. Zatem wystarczy sprawdzić zbieżność szeregu [tex]\Sigma_{n=1}^\infty(-1)^n*\frac{1}{n}[/tex]. W tym przypadku [tex]a_n=\frac{1}{n}[/tex].

Sprawdzamy, czy ten ciąg spełnia warunki kryterium.

1) Czy jest malejący?

[tex]a_{n+1}-a_n=\frac{1}{n+1}-\frac{1}{n}=\frac{n}{n(n+1)}-\frac{n+1}{n(n+1)}=\frac{n-n-1}{n(n+1)}=\frac{-1}{n(n+1)} < 0[/tex]

Jest malejący.

2) Czy jest nieujemny?

[tex]a_n=\frac{1}{n} > 0[/tex]

Jest nieujemny.

3) Czy jest zbieżny do 0?

[tex]\lim_{n \to \infty} \frac{1}{n}=[\frac{1}{+\infty}]=0[/tex]

Jest zbieżny do 0.

Wniosek:

Ciąg [tex]a_n=\frac{1}{n}[/tex] spełnia warunki kryterium Leibniza, więc szereg [tex]\Sigma_{n=1}^\infty(-1)^n*\frac{1}{n}[/tex] jest zbieżny, wiec zbieżny jest również szereg [tex]\Sigma_{n=1}^\infty(-1)^n*(-\frac{1}{n})[/tex].