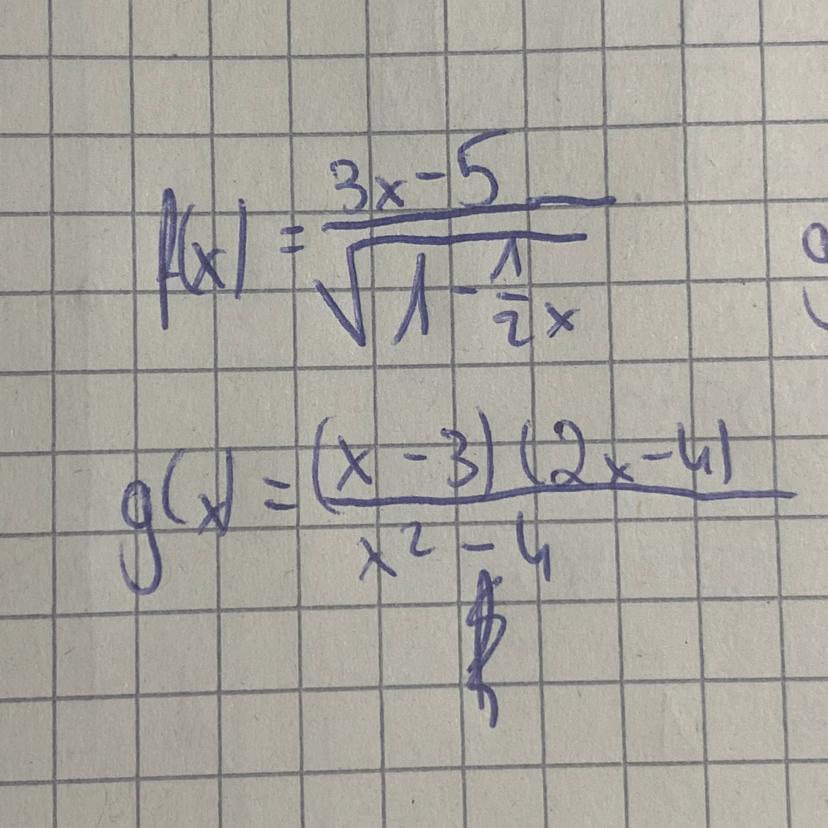pls pomóżcieeeeeeeeee
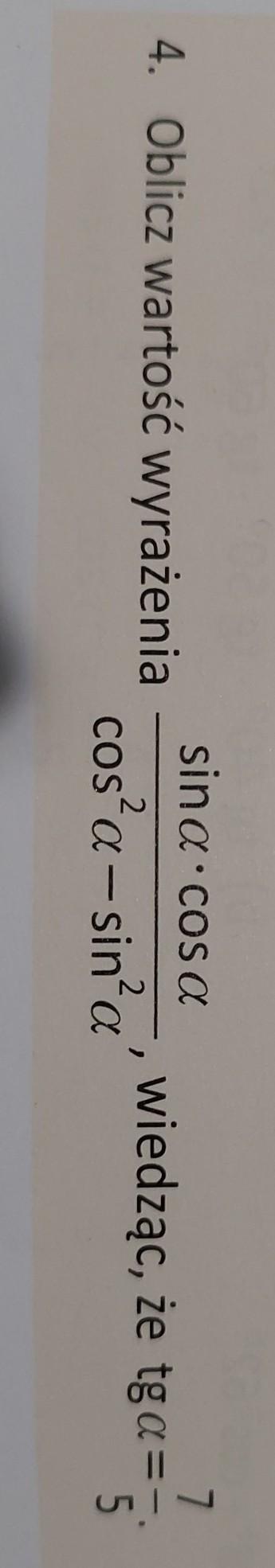
-
Temat:
Matematyka -
Autor:
emilee -
Utworzono:
1 rok temu
Odpowiedzi 1
Odpowiedź:
[tex]\frac{sin \alpha *cos \alpha }{cos^2\alpha - sin^2\alpha } =[/tex] dzielimy licznik i mianownik przez cos² α
= [tex]\frac{tg \alpha }{1 - tg^2\alpha }[/tex] = [tex]\frac{\frac{7}{5} }{1 - \frac{49}{25} }[/tex] = [tex]\frac{7}{5} : \frac{- 24}{25}[/tex] = [tex]\frac{7}{5}* ( - \frac{25}{24}[/tex] ) = - [tex]\frac{35}{24}[/tex]
Szczegółowe wyjaśnienie:
-
Autor:
blackiehamilton
-
Oceń odpowiedź:
3
Znasz odpowiedź? Dodaj ją tutaj!
Wybierz język i region
How much to ban the user?
1 hour
1 day
100 years