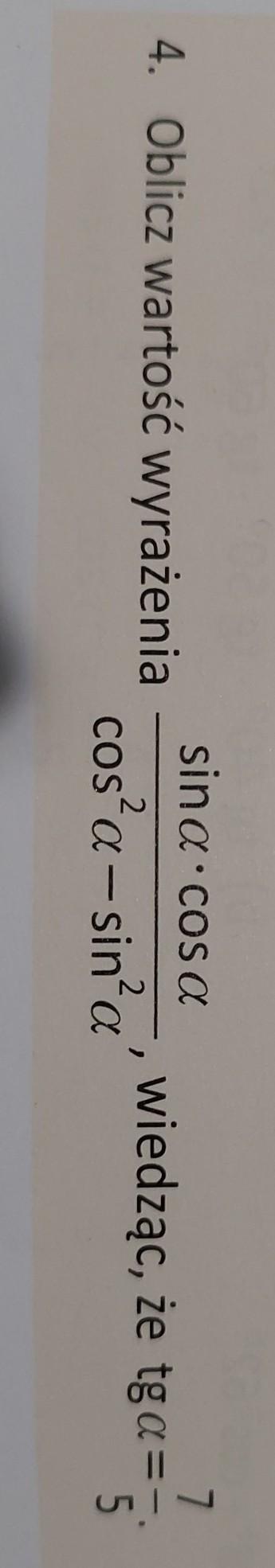Proszę na jutro! Zadanie 3, 4, 5 i 6. Matematyka klasa 5 podręcznik z plusem GWO (gdańskie wydawnictwo oświatowe). Była bym wdzięczna. Z góry pozdrawiam i dziękuję :)

-
Temat:
Matematyka -
Autor:
jamarcuscantu -
Utworzono:
1 rok temu
Odpowiedzi 1
Odpowiedź:
ZADANIE 3
a) -4
b) -12
c) -6
d) 1
e) -7
f) 18
ZADANiE 4
a) 7
b) 4
c) 6
d) 3
e) (-7)
f) 0
ZADANIE 5
a) u
b) w
c) w
ZADANIE 6
a) np. (-7) (-8) (-2) (-3) (-1)
b) np. (-6) (-7) (-8) (-9) (-10)
c) np.(-8) (-10) (-18) (-40) (-13)
Mam nadzieję że pomogłam
-
Autor:
shylavilla
-
Oceń odpowiedź:
7
Znasz odpowiedź? Dodaj ją tutaj!
Wybierz język i region
How much to ban the user?
1 hour
1 day
100 years