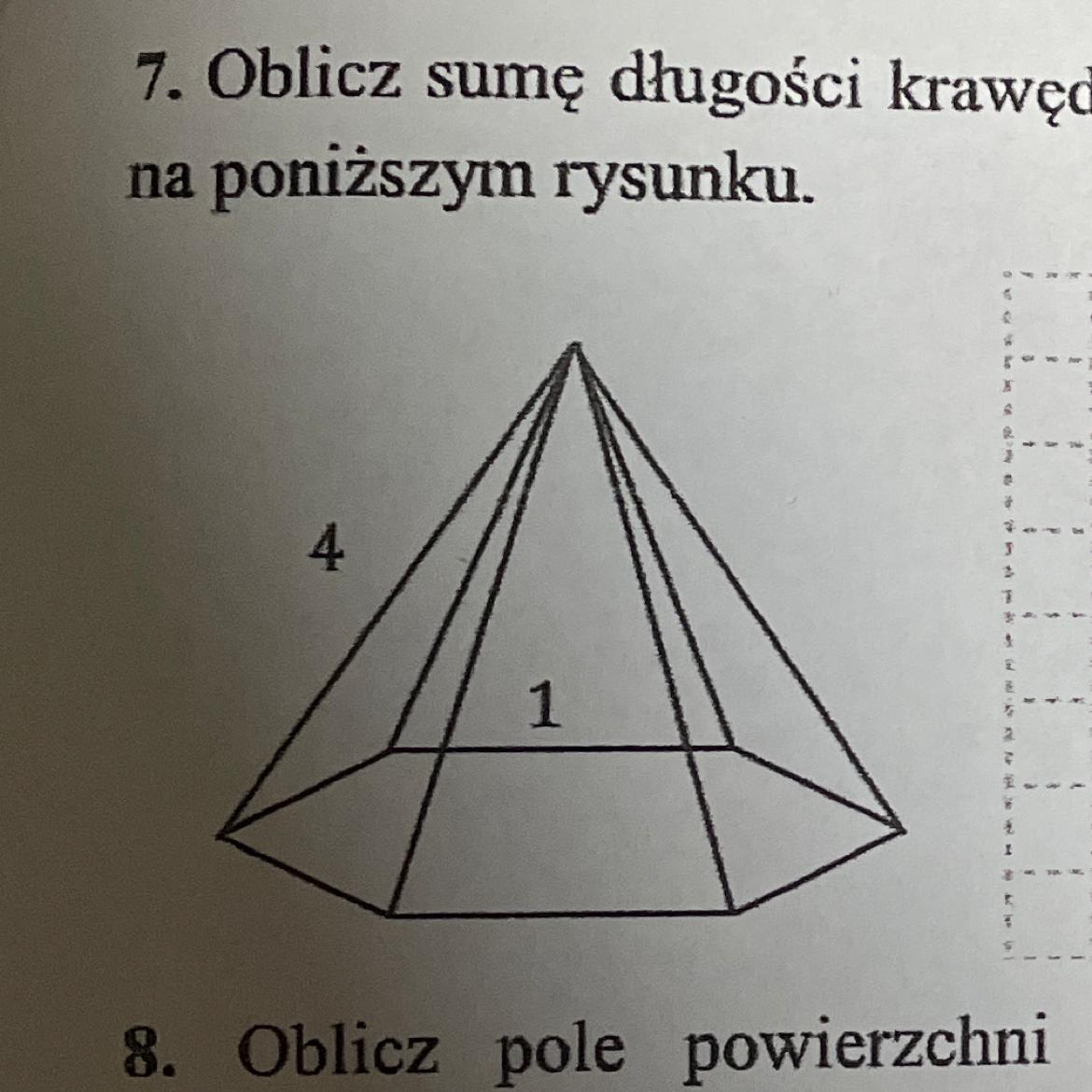
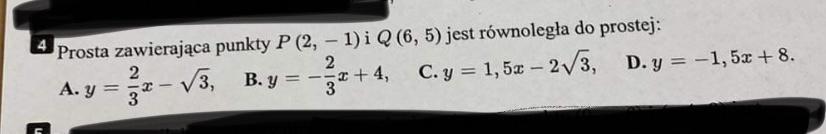Proszę jak najszybciej// zadanie 1 i 2. (trzeciego nie trzeba robić)

Do rozwiązania mamy równania wymierne w większości przedstawione w postaci proporcji.

Proporcja jest to równość ilorazów. Rozwiązuje się ją mnożąc na krzyż.

Przy równaniach wymiernych należy pamiętać o określeniu dziedziny (mianownik nie może być równy 0).

[tex]a)\\\bold{D}:x\neq0\ \wedge\ 2+x\neq0\\\\\boxed{\bold{x\in\mathbb{R}-\{-2,\ 0\}}}\\\\\dfrac{4}{x}=\dfrac{3}{2+x}\\\\4(2+x)=x\cdot 3\\\\8+4x=3x\qquad|-8-3x\\\\\huge\boxed{x=-8}\in\bold{D}[/tex]

[tex]b)\\\bold{D}:x+2\neq0\ \wedge\ x-3\neq0\\\\\boxed{\bold{D:x\in\mathbb{R}-\{-2,\ 3\}}}[/tex]

[tex]\dfrac{2}{x+2}-\dfrac{1}{x-3}=0\\\\\dfrac{2}{x+2}=\dfrac{1}{x-3}\\\\2(x-3)=1(x+2)\\\\2x-6=x+2\qquad|+6-x\\\\\huge\boxed{x=8}\in\bold{D}[/tex]

[tex]c)\\\bold{D}:x-1\neq0\ \wedge\ x\neq0\\\\\boxed{\bold{D:x\in\mathbb{R}-\{0,\ 1\}}}\\\\\dfrac{x}{x-1}=\dfrac{x+2}{x}\\\\x\cdot x=(x-1)(x+2)\\\\x^2=x^2+2x-x-2\qquad|-x^2\\\\0=x-2\qquad|+2\\\\\huge\boxed{x=2}\in\bold{D}[/tex]

[tex]d)\\\bold{D}:x-2\neq0\ \wedge\ x+2\neq0\\\\\boxed{\bold{D:x\in\mathbb{R}-\{-2,\ 2\}}}\\\\\dfrac{x-3}{x-2}=\dfrac{x+3}{x+2}\\\\(x-3)(x+2)=(x-2)(x+3)\\\\x^2+2x-3x-6=x^2+3x-2x-6\qquad|+6-x^2\\\\-x=x\qquad|-x\\\\-2x=0\qquad|:(-2)\\\\\huge\boxed{x=0}\in\bold{D}[/tex]

[tex]e)\\\bold{D}:x\neq0\ \wedge\ 2x+1\neq0\\\\\boxed{\bold{D:x\in\mathbb{R}-\left\{-\dfrac{1}{2},\ 0\right\}}}\\\\\dfrac{x+1}{x}=\dfrac{x+1}{2x+1}\\\\(x+1)(2x+1)=x(x+1)\\\\2x^2+x+2x+1=x^2+x\\\\2x^2+3x+1=x^2+x\qquad|-x^2-x\\\\x^2+2x+1=0[/tex]

Możemy zauważyć, że jest to rozwinięcie wzoru skróconego mnożenia:

(a + b)² = a² + 2ab + b²

[tex]x^2+2\cdot x\cdot 1+1^2=0\\\\(x+1)^2=0\iff x+1=0\qquad|-1\\\\\huge\boxed{x=-1}\in\bold{D}[/tex]

[tex]f)\\\bold{D}:\ 2x-1\neq0\ \wedge\ x\neq0\\\\\boxed{\bold{D:x\in\mathbb{R}-\left\{0,\ \dfrac{1}{2}\right\}}}\\\\\dfrac{x+1}{2x-1}-\dfrac{2}{x}=0\\\\\dfrac{x+1}{2x-1}=\dfrac{2}{x}\\\\x(x+1)=2(2x-1)\\\\x^2+x=4x-2\qquad|-4x+2\\\\x^2-3x+2=0\\\\x^2-x-2x+2=0\\\\x(x-1)-2(x-1)=0\\\\(x-1)(x-2)=0\iff x-1=0\ \vee\ x-2=0\\\\\huge\boxed{x=1\ \vee\ x=2}\in\bold{D}[/tex]

[tex]a)\\\bold{D}:x+2\neq0\\\\\boxed{\bold{D:x\in\mathbb{R}-\{-2\}}}\\\\\dfrac{x}{-3}=\dfrac{-5}{x+2}\\\\x(x+2)=(-3)\cdot(-5)\\\\x^2+2x=15\qquad|+1\\\\x^2+2x+1=16\qquad/(a+b)^2=a^2+2ab+b^2\\\\(x+1)^2=16\Rightarrow x+1=\pm\sqrt{16}\\\\x+1=-4\ \vee\ x+1=4\qquad|-1\\\\\huge\boxed{x=-5\ \vee\ x=3}\in\bold{D},\mathbb{Z}[/tex]

[tex]b)\\\bold{D}:2x\neq0\\\\\boxed{\bold{D:x\in\mathbb{R}-\{0\}}}\\\\x=\dfrac{5x+3}{2x}\\\\\dfrac{x}{1}=\dfrac{5x+3}{2x}\\\\x\cdot 2x=1(5x+3)\\\\2x^2=5x+3\qquad|-5x-3\\\\2x^2-5x-3=0\\\\2x^2-6x+x-3=0\\\\2x(x-3)+1(x-3)=0\\\\(x-3)(2x+1)=0\iff x-3=0\ \vee\ 2x+1=0\\\\\huge\boxed{x=3}\in\bold{D},\mathbb{Z}\ \vee\ x=-\dfrac{1}{2}\in\bold{D},\not\in\mathbb{Z}[/tex]

[tex]c)\\\bold{D}:x-1\neq0\\\\\boxed{\bold{D:x\in\mathbb{R}-\{1\}}}\\\\x+1=\dfrac{2-2x}{x-1}\\\\x+1=\dfrac{-2(x-1)}{x-1}\\\\x+1=-2\qquad|-1\\\\\huge\boxed{x=-3}\in\bold{D},\mathbb{Z}[/tex]

[tex]d)\\\bold{D}:x\neq0\ \wedge\ x+3\neq0\\\\\boxed{\bold{D:x\in\mathbb{R}-\{-3,\ 0\}}}\\\\1-\dfrac{1}{x}=\dfrac{x+1}{x+3}\\\\\dfrac{x}{x}-\dfrac{1}{x}=\dfrac{x+1}{x+3}\\\\\dfrac{x-1}{x}=\dfrac{x+1}{x+3}\\\\(x-1)(x+3)=x(x+1)\\\\x^2+3x-x-3=x^2+x\qquad|-x^2\\\\2x-3=x\qquad|+3-x\\\\\huge\boxed{x=3}\in\bold{D},\mathbb{Z}[/tex]

[tex]e)\\\bold{D}:2-3x\neq0\\\\\boxed{\bold{D:x\in\mathbb{R}-\left\{\dfrac{2}{3}\right\}}}\\\\\dfrac{6x-4}{2-3x}=-2x\\\\\dfrac{6x-4}{2-3x}=\dfrac{-2x}{1}\\\\1(6x-4)=-2x(2-3x)\\\\6x-4=-4x+6x^2\qquad|+4x-6x^2\\\\-6x^2+10x-4=0\\\\-6x^2+6x+4x-4=0\\\\-6x(x-1)+4(x-1)=0\\\\(x-1)(4-6x)=0\iff x-1=0\ \vee\ 4-6x=0\\\\\huge\boxed{x=1}\in\bold{D},\mathbb{Z}\ \vee\ x=\dfrac{2}{3}\in\bold{D},\not\in\mathbb{Z}[/tex]

[tex]f)\\\bold{D}:x\neq0\\\\\boxed{\bold{D:x\in\mathbb{R}-\{0\}}}\\\\6x+1=\dfrac{2}{x}\\\\\dfrac{6x+1}{1}=\dfrac{2}{x}\\\\x(6x+1)=1\cdot2\\\\6x^2+x=2\qquad|-2\\\\6x^2+x-2=0\\\\6x^2+4x-3x-2=0\\\\2x(3x+2)-1(3x+2)=0\\\\(3x+2)(2x-1)=0\iff3x+2=0\ \vee\ 2x-1=0\\\\x=-\dfrac{2}{3}\in\bold{D},\notin\mathbb{Z}\ \vee\ x=\dfrac{1}{2}\in\bold{D},\notin\mathbb{Z}[/tex]