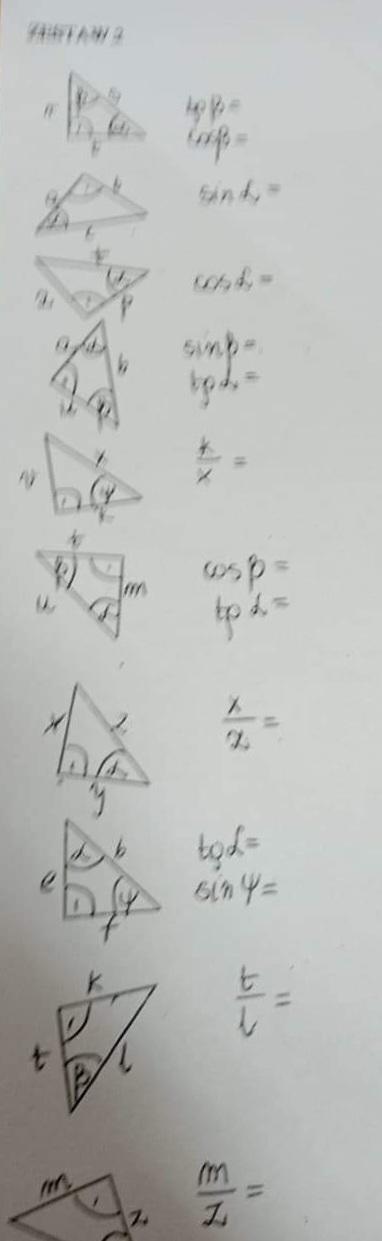Proszę o rozwiązanie

-
Temat:
Matematyka -
Autor:
marley76 -
Utworzono:
1 rok temu
Odpowiedzi 1
Odpowiedź:
[tex]a)\ \ 3\frac{1}{2}+2\frac{2}{3}=3\frac{3}{6}+2\frac{4}{6}=5\frac{7}{6}=6\frac{1}{6}\\\\b)\ \ 4\frac{3}{5}+2\frac{3}{4}=4\frac{12}{20}+2\frac{15}{20}=6\frac{27}{20}=7\frac{7}{20}\\\\c)\ \ 7\frac{2}{3}-5\frac{5}{6}=7\frac{4}{6}-5\frac{5}{6}=6\frac{10}{6}-5\frac{5}{6}=1\frac{5}{6}\\\\d)\ \ 4-1\frac{3}{5}=3\frac{5}{5}-1\frac{3}{5}=2\frac{2}{5}[/tex]
-
Autor:
maemfuk
-
Oceń odpowiedź:
3
Znasz odpowiedź? Dodaj ją tutaj!
Wybierz język i region
How much to ban the user?
1 hour
1 day
100 years