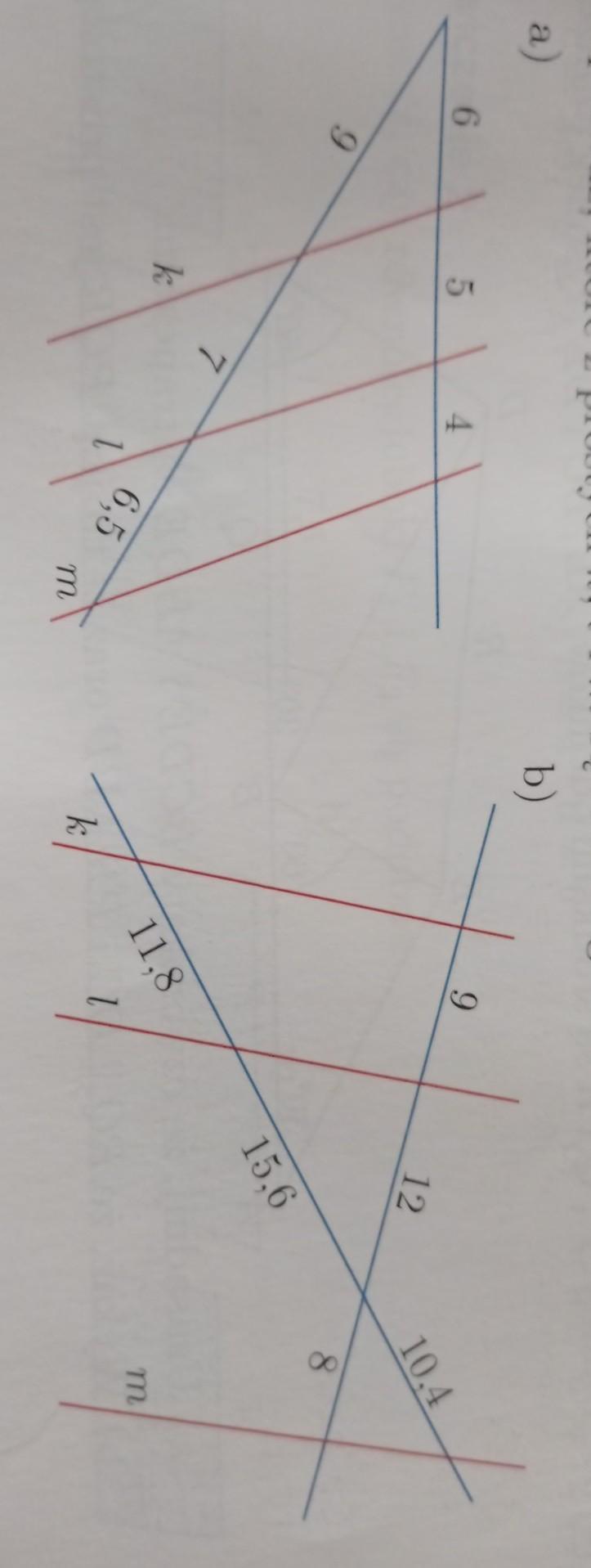
a) Tylko prosta k i m są do siebie równoległe.b) Tylko prosta l i m są do siebie równoległe.
W zadaniu skorzystamy z twierdzenia odwrotnego do twierdzenia Talesa:
Jeżeli odcinki, które powstały w wyniku przecięcia prostych na jednym ramieniu kąta są proporcjonalne do odpowiednich odcinków na drugim ramieniu kąta to wynika z tego, że podane proste są do siebie równoległe.
a)
[tex]\cfrac{6}{9} = \cfrac{6+5}{9+7} \\\\\cfrac{2}{3} = \cfrac{11}{16} \\\\[/tex]
Mnożymy na krzyż i otrzymujemy:
[tex]33\neq 32[/tex]
Proste k i l nie są do siebie równoległe.
[tex]\cfrac{6}{9} = \cfrac{6+5+4}{9+7+6,5} \\\\\cfrac{2}{3} = \cfrac{15}{22,5} \\\\[/tex]
Mnożymy na krzyż i otrzymujemy:
[tex]45 = 45[/tex]
Proste k i m są do siebie równoległe.
[tex]\cfrac{6+5}{9+7} = \cfrac{6+5+4}{9+7+6,5} \\\\\cfrac{11}{16} = \cfrac{15}{22,5} \\\\16 \cdot 15 = 11 \cdot 22,5 \\\\240 \neq 247,5[/tex]
Proste l i m nie są do siebie równoległe.
b)
[tex]\cfrac{9+12}{11,8+15,6} = \cfrac{12}{15,6} \\\\\cfrac{21}{27,4} = \cfrac{12}{15,6} \\\\27,4 \cdot 12 = 21 \cdot 15,6 \\\\328,8 \neq 327,6 \\\\[/tex]
Proste k i l nie są do siebie równoległe.
[tex]\cfrac{9}{11,8} = \cfrac{8}{10,4} \\\\11,8 \cdot 8 = 9 \cdot 10,4 \\\\94,4 \neq 93,6[/tex]
Proste k i m nie są do siebie równoległe.
[tex]\cfrac{12}{15,6} = \cfrac{8}{10,4} \\\\15,6 \cdot 8 =12 \cdot 10,4 \\\\124,8 = 124,8[/tex]
Proste l i m są do siebie równoległe.
#SPJ1