3. Przyprostokątne trójkąta prostokątnego mają długości 6 cm i 8 cm. Uzasadnij, że wysokość poprowadzona z wierzchołka kąta prostego dzieli ten trójkąt na trójkąty podobne, a następnie oblicz długość tej wysokości.
-
Temat:
Matematyka -
Autor:
freckles -
Utworzono:
1 rok temu
Odpowiedzi 1
Szczegółowe wyjaśnienie:
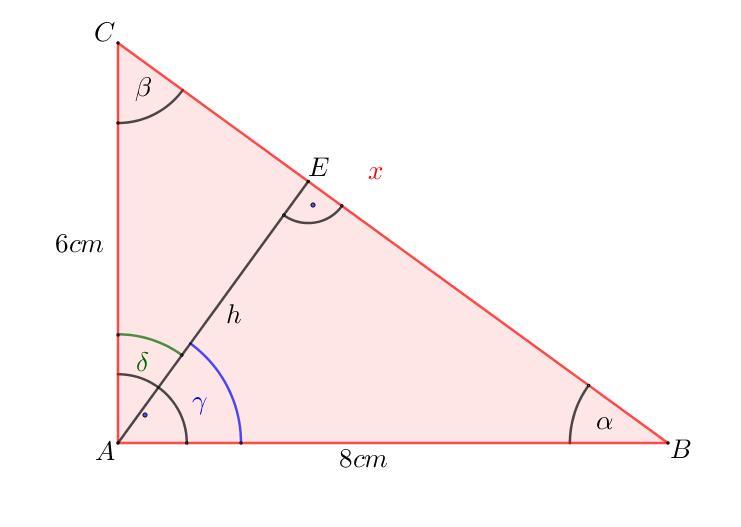
Rysunek poglądowy w załączniku.
Aby wykazać, że trójkąty prostokątne ABE i CAE są podobne wystarczy wskazać, że jeden z kątów ostrych w jednym trójkącie ma tą samą miarę co kąt w drugim.
Wiemy, że suma miar kątów ostrych w trójkącie prostokątnym wynosi 90°.
Stąd:
[tex]\alpha+\beta=90^o\\\\\alpha+\gamma=90^o\\\\\beta+\delta=90^o[/tex]
Stąd wnioskujemy, że:
[tex]\gamma=\beta\ \wedge\ \delta=\alpha[/tex]
Zatem na podstawie cechy podobieństwa trójkątów KK (kąt-kąt) mamy, że
[tex]\triangle ABC\sim\triangle EBA\sim\triangle EAC[/tex]
[tex]\blacksquare[/tex]
Obliczmy długość przeciwprostokątnej trójkąta ABC korzystając z twierdzenia Pitagorasa:
[tex]x^2=6^2+8^2\\\\x^2=36+64\\\\x^2=100\to x=\sqrt{100}\\\\x=10(cm)[/tex]
Z podobieństwa trójkątów ABC i EBA obliczamy długość wysokości [tex]h[/tex]:
[tex]\dfrac{|AB|}{|BC|}=\dfrac{|AE|}{|AC|}[/tex]
podstawiamy:
[tex]\dfrac{8}{10}=\dfrac{h}{6}\qquad|\cdot6\\\\h=\dfrac{48}{10}\\\\h=4,8(cm)[/tex]
-
Autor:
leeq5ur
-
Oceń odpowiedź:
7