Cześć! Potrzebuję pomocy z matematyki Z dwoma zadaniami. Jedno zadanie dotyczy podania pierwszych 3 członów w szeregu Taylora zaś drugie dotyyczy obliczenia puunktów krytycznych funkcji. Zadania są w załączniku. Bardzo ale to bardzo proszę o pomoc i jakiś odzew, zależy mi na tym aby porównać i sprawdzić mój sposób myslenia dlatego liczę,że ktoś dobrze rozwiąże oba zadania. Daję wszystkie punkty jakie mam.
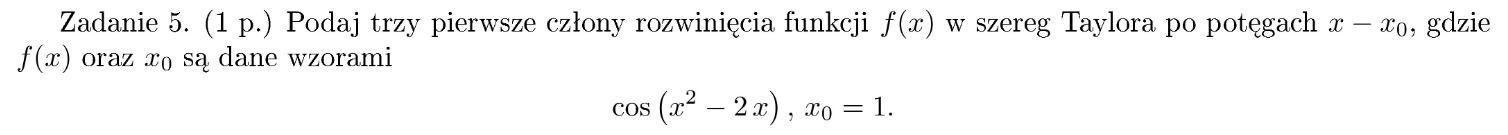
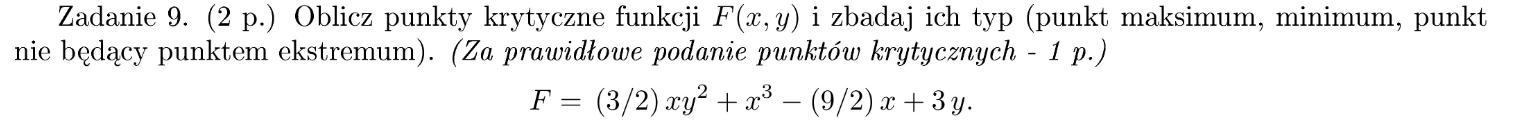
-
Temat:
Matematyka -
Autor:
edith -
Utworzono:
1 rok temu
Odpowiedzi 1
zad2:
Warunkiem koniecznym, żeby w punkcie P było ekstremum jest zerowanie się pochodnych cząstkowych, czyli:
[tex]\frac{\partial f}{\partial x} = \frac{3y^{2}}{2} + 3x^{2} - \frac{9}{2} = 0\\\frac{\partial f}{\partial y} = 3xy +3 =0\\[/tex]
Z tego układu otrzymujemy punkty:
[tex]P_{1} = (-1,1)\\P_{2} = (1,-1)\\P_{3} = (\frac{-1}{\sqrt{2}}, \sqrt{2})\\P_{4} = (\frac{1}{\sqrt{2}}, -\sqrt{2})[/tex]
Teraz liczymy drugie pochodne:
[tex]\frac{\partial^{2}f}{\partial x\partial y} = 3y = \frac{\partial^{2}f}{\partial y\partial x}\\\frac{\partial^{2}f}{\partial x^{2}} = 6x\\\frac{\partial^{2}f}{\partial y^{2}} = 3x[/tex]
Czyli macierz Hessego wygląda tak:
[tex]\begin{bmatrix}6x & 3y \\3y & 3x \end{bmatrix}[/tex]
Wyznacznik pierwszego minora:
[tex]H_{1} = 6x[/tex]
i 2 minora:
[tex]H_{2} = 18x^{2} - 9 y^{2} = 9(2x^{2} - y^{2})[/tex]
Dalej wystarczy podstawić otrzymane wcześniej punkty,
jeśli [tex]H_{1}(P)\ i\ H_{2}(P)[/tex] są obie dodatnio określone (większe od 0) to w punkcie P jest minimum lokalne
jeśli [tex]H_{1}(P)[/tex] jest ujemnie określone (<0) oraz [tex]H_{2}(P)[/tex] jest dodatnio określone (>0) to w punkcie P jest maximum lokalne
ogólnie dla wielu zmiennych:
minimum lokalne gdy każdy z minorów > 0
max lokalne: gdy znaki minorów są na przemian ujemne i dodatnie (- + - + - + itd.) ważne: dla znaków (+ - + - + -) nie ma ekstremum w danym punkcie
jeśli któreś z [tex]H_{1},\ H_{2}[/tex] jest 0, to w punkcie P może(ale nie musi) być ekstremum, a jeśli któryś ze znaków się nie zgadza to w punkcie P na pewno nie ma ekstremum lokalnego
[tex]P_1:\\H_{1} = 6 > 0\\h_{2} = 9 > 0[/tex](++), czyli w [tex]P_{1}[/tex] jest minimum lokalne
[tex]P_{2}:\\H_{1} = -6 < 0\\H_{2} = 9[/tex](-+), czyli w [tex]P_{2}[/tex] jest max lokalne
[tex]P_{3}:\\H_{1} < 0\\H_{2} = 9(1 - 2) < 0[/tex] (- -), w [tex]P_{3}[/tex] nie ma ekstremum lokalnego
[tex]P_{4}:\\H_{1} > 0\\H_{2} = 9(1-2) < 0[/tex] (+ -), w [tex]P_{4}[/tex] nie ma ekstremum lokalnego
-
Autor:
maemfuk
-
Oceń odpowiedź:
6
