Na teraz daje naj pilneee!

-
Temat:
Matematyka -
Autor:
syllable -
Utworzono:
1 rok temu
Odpowiedzi 1
Zad. 1 - za slaba jakosc zdjecia
Zad. 2
[tex]\left[\begin{array}{cccccc}x&-2&-1&0&1&2\\f(x)&8&2&0&2&8\end{array}\right][/tex]
g(x) - funkcja f przesunieta o 3 jednostki w prawo
h(x) - funkcja f przesunieta o 2 jednostki w gore
Zad. 3
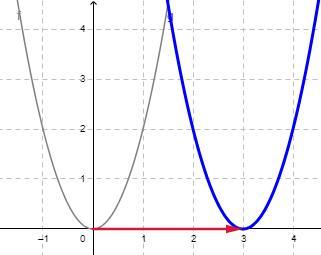
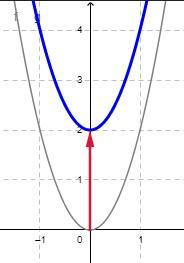
-
Autor:
bubble buttqfvm
-
Oceń odpowiedź:
9
Znasz odpowiedź? Dodaj ją tutaj!
Wybierz język i region
How much to ban the user?
1 hour
1 day
100 years

