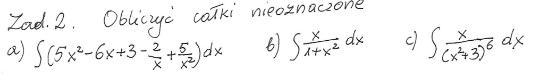Szereg Taylora ktoś pomoże, z góry dziękuję :)
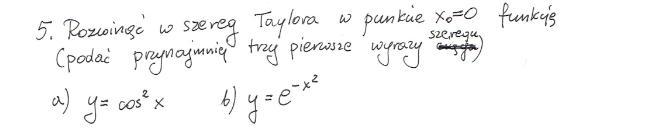
-
Temat:
Matematyka -
Autor:
ball -
Utworzono:
1 rok temu
Odpowiedzi 1
Rozwiązanie:
Szereg Taylora:
[tex]$f(x)=\sum^{\infty}_{n=0} \frac{f^{(n)}(x_{0})(x-x_{0})^{n}}{n!}[/tex]
W przypadku [tex]x_{0}=0[/tex] szereg określony jest wzorem:
[tex]$f(x)=\sum^{\infty}_{n=0} \frac{f^{(n)}(0)}{n!}x^{n}[/tex]
[tex]\bold{(a)}[/tex]
[tex]y=\cos^{2}x[/tex]
Kilka pierwszych pochodnych:
[tex]y'=-2\cos x \sin x=-\sin2x[/tex]
[tex]y''=-2\cos 2x[/tex]
[tex]y^{(3)}=4 \sin 2x[/tex]
[tex]y^{(4)}=-8 \cos 2x[/tex]
Zatem:
[tex]$\cos^{2}x=\frac{\cos(0)}{0!}x^{0} -\frac{\sin(0)}{1!}x-\frac{2\cos(0)}{2!}x^{2}+\frac{4 \sin (0)}{3!} x^{3}+\frac{8\cos 2x}{4!}x^{4} +...=[/tex]
[tex]$=1 -x^{2} +\frac{x^{4}}{3} +...[/tex]
Aby znaleźć zapis z użyciem sumy, można posłużyć się dobrze znanym rozwinięciem funkcji [tex]\cos x[/tex] w szereg Maclaurina:
[tex]$\cos x=\sum^{\infty}_{n=0} \frac{(-1)^{n}}{(2n)!} x^{2n}[/tex]
Teraz wystarczy zauważyć, że:
[tex]$\cos^{2}x=\frac{1+\cos 2x}{2} =\frac{1}{2} +\frac{\cos 2x}{2} =\frac{1}{2}+\frac{1}{2}\sum^{\infty}_{n=0}\frac{(-1)^{n}}{(2n)!} (2x)^{2n}=[/tex]
[tex]$=1+\sum^{\infty}_{n=1}\frac{(-1)^{n} \cdot 2^{2n-1}}{(2n)!}x^{2n}[/tex]
[tex]\bold{(b)}[/tex]
[tex]$y=e^{-x^{2}}[/tex]
Tutaj nawet szkoda liczyć pochodnych, lepiej od razu postarajmy się zapisać to z użyciem sumy. Użyjemy znanego rozwinięcia:[tex]$e^{x}=\sum^{\infty}_{n=0}\frac{x^n}{n!}[/tex]
Mamy:
[tex]$e^{-x^{2}}=\sum^{\infty}_{n=0}\frac{(-x^{2})^{n}}{n!} =\sum^{\infty}_{n=0}\frac{(-1)^{n}}{n!} x^{2n}[/tex]
Teraz możemy zapisać pierwsze trzy wyrazy:
[tex]$e^{-x^{2}}=1-x^{2}+\frac{x^{4}}{2}+...[/tex]
-
Autor:
evelingmal
-
Oceń odpowiedź:
8