Proszę rozwiązać to zadanie.

-
Temat:
Matematyka -
Autor:
ryleebartlett -
Utworzono:
1 rok temu
Odpowiedzi 1
Rozwiązanie:
Całka:
[tex]$\iiint\limits^{}_{V}x^{2}dxdydz[/tex]
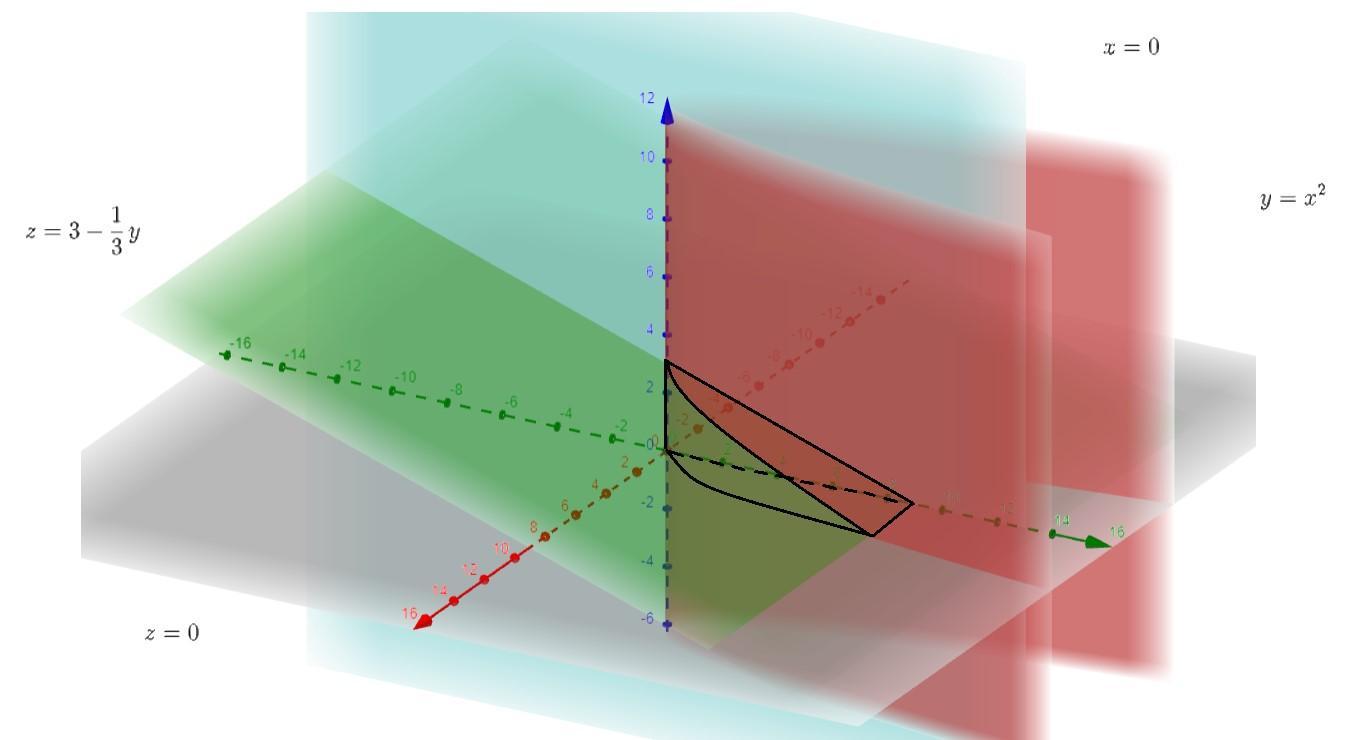
Rysunek w załączniku (wzięto jeden z możliwych obszarów, ale nie ma to znaczenia ze względu na symetrię).
Na początek musimy wyznaczyć granice całkowania. Z rysunku łatwo widzimy, że:
[tex]0\leq x\leq \sqrt{y}[/tex]
Wyznaczamy dla jakiego [tex]y[/tex] płaszczyzna [tex]$z=3-\frac{1}{3}y[/tex] przecina płaszczyznę [tex]z=0[/tex] :
[tex]$3-\frac{1}{3}y=0 \iff y=9[/tex]
Zatem:
[tex]0\leq y\leq 9[/tex]
Z polecenia:
[tex]$0\leq z\leq 3-\frac{1}{3}y[/tex]
Ostatecznie:
[tex]$V=\Big\{(x,y,z) \in \mathbb{R}^{3}:0\leq x\leq \sqrt{y} \wedge 0\leq y\leq 9 \wedge 0\leq z\leq 3-\frac{1}{3}y \Big\}[/tex]
Całka:
[tex]$\iiint\limits^{}_{V}x^{2}dxdydz=\int\limits^{9}_{0} \ \int \limits^{\sqrt{y}}_{0} \ \int\limits^{3-\frac{1}{3}y}_{0} x^{2} \ dzdxdy=\int\limits^{9}_{0}\int \limits^{\sqrt{y}}_{0}x^{2}\Big(3-\frac{1}{3}y\Big) \ dxdy=[/tex]
[tex]$=\int\limits^{9}_{0} \Big(3-\frac{1}{3}y\Big) \int\limits^{\sqrt{y}}_{0}x^{2} \ dxdy=\int\limits^{9}_{0}\Big(3-\frac{1}{3}y\Big) \frac{y^{\frac{3}{2}}}{3} \ dy=\int\limits^{9}_{0}y^{\frac{3}{2}}-\frac{y^{\frac{5}{2}}}{9} \ dy=[/tex]
[tex]$=\frac{2}{5}y^{\frac{5}{2}}-\frac{2}{63}y^{\frac{7}{2}}\Bigg|^{9}_{0}=\frac{972}{35}[/tex]
Można też od razu przejść na całkę podwójną określając obszar całkowania [tex]D[/tex] płaszczyźnie.
-
Autor:
mikew6r9
-
Oceń odpowiedź:
18
