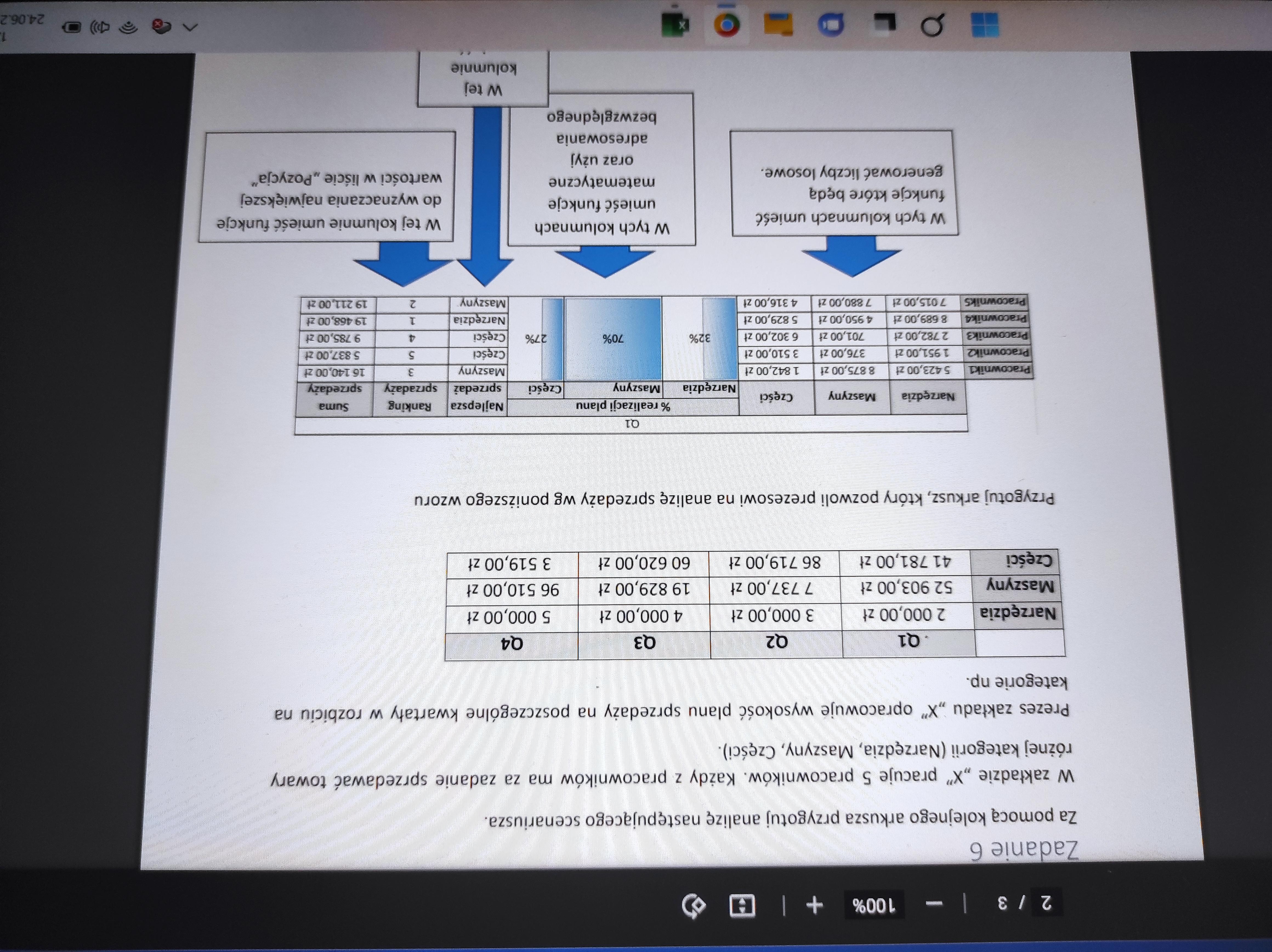
Zadanie w załączniku
-
Temat:
Matematyka -
Autor:
sandra46 -
Utworzono:
1 rok temu
Odpowiedzi 1
W każdym wypadku stosuję współrzędne biegunowe:
[tex]x=r\cos\phi\\y=r\sin\phi\\\det J=r[/tex]
b)
obszar całkowania:
[tex]x^2+y^2=r^2\leq1\\0\leq r\leq 1\\x,y\geq0,\ 0\leq\phi\leq\pi/2[/tex]
[tex]\int_0^1{\ln{(r^2+1)}r\,dr}\int_{0}^{\pi/2}{d\phi}=\frac{\pi}{2}\int_0^1{\ln{(r^2+1)}r\,dr}\\r^2+1=a\\2r\,dr=da\\\frac{\pi}{2}\int_{1}^{2}{\ln{a}\,\frac{da}{2}}[/tex]
całkę tę dobrze liczy się przez części:
[tex]u=\ln{a},\ dv=da\\du=\frac{da}{a},\ v=a\\\frac{\pi}{4}a\ln{a}|_1^2-\frac{\pi}{4}\int_1^2{da}=\frac{\pi}{4}(2\ln{2}-1)[/tex]
c)
Obszar całkowania:
[tex]x^2+y^2=r^2\leq 4\\0\leq r\leq 2[/tex]
[tex]\int_0^{2\pi}{d\phi}\int_0^2{(4-2r\cos\phi-3r\sin\phi)r\,dr}=\int_0^{2\pi}{(2r^2-\frac{2}{3}r^3\cos\phi-r^3\sin\phi)|_0^2d\phi}=\\=\int_0^{2\pi}{(8-\frac{16}{3}\cos\phi-8\sin\phi)\,d\phi}=16\pi[/tex]
całki z sinusa i cosinusa po kącie pełnym dają zero
pozdrawiam
-
Autor:
bernarda7mkj
-
Oceń odpowiedź:
10
Znasz odpowiedź? Dodaj ją tutaj!
Other related questions that may help you
-
Autor:
cody47
Odpowiedź:
Arkusz w załączniku
Wyjaśnienie:
Nie widzę całego polecenia więc zrobiłem tyle ile widać na obrazku i losuje liczby od 0 do 10000 tylko że dla 4 kwartałów a nie jednego. I na obrazku coś jest nie tak z tym % realizacji planu tzn, jest 70% a zajmuje całą szerokość albo 32% na prawie połowę
-
Autor:
angel527
-
Oceń odpowiedź:
3
-
Autor:
reyes
-
Autor:
tobyzorj
-
Oceń odpowiedź:
3
-
Autor:
compton
-
Autor:
probocortez
-
Oceń odpowiedź:
9