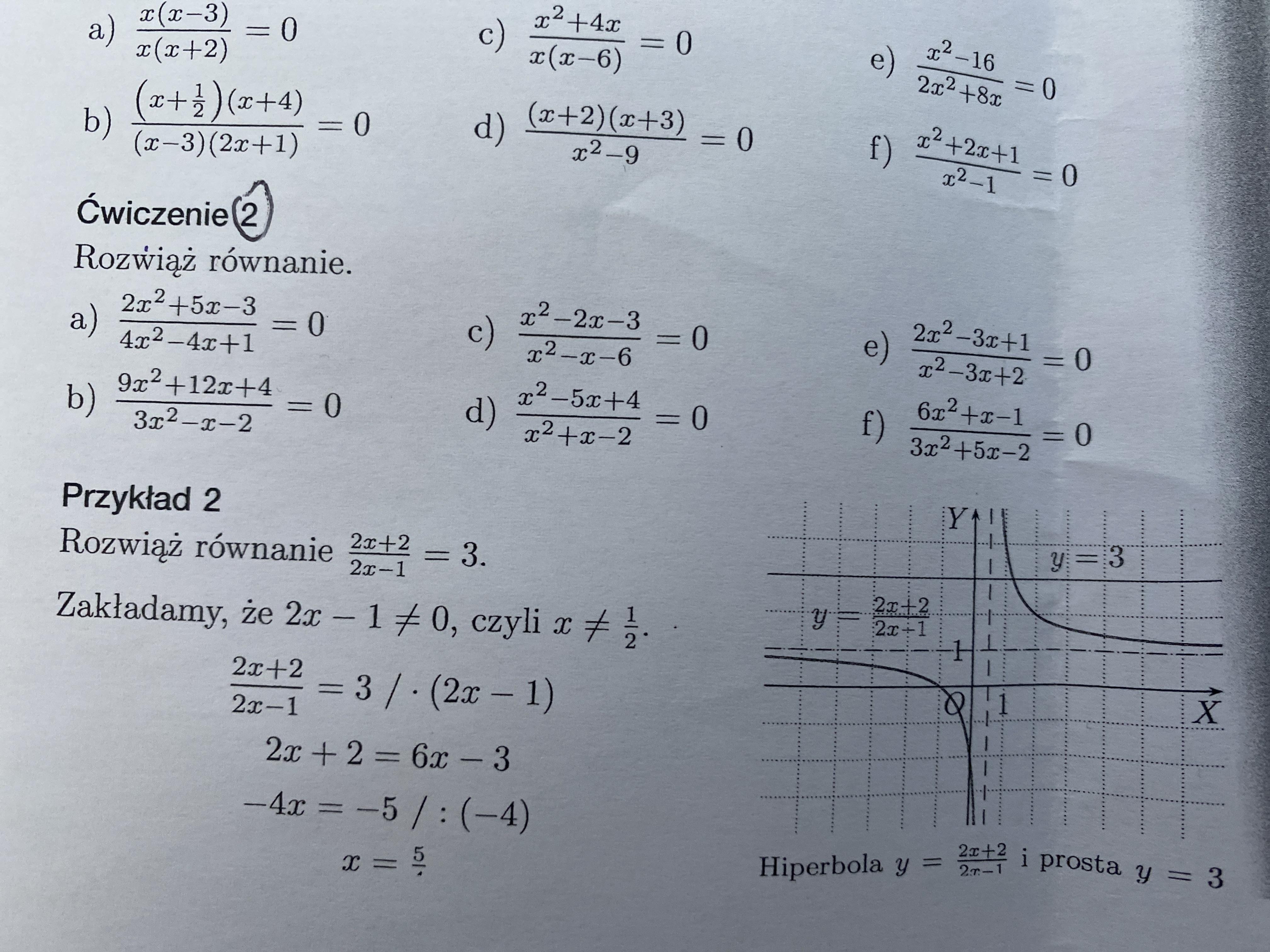Równania wymierne Zadanie 1
-
Temat:
Matematyka -
Autor:
maia -
Utworzono:
1 rok temu
Odpowiedzi 2
[tex]a)\\\\\frac{4}x=\frac{3}{2+x}\\\\x\neq 0\\2+x\neq 0\\x\neq -2\\\\x\in R/ \{0, -2\}\\\\4(2+x)=3x\\8+4x=3x\\4x-3x=-8\\x=-8[/tex]
[tex]b)\\\\\frac2{x+2}-\frac{1}{x-3}=0\\\\\\x+2 \neq 0\\x\neq -2\\\\x-3\neq 0\\x\neq 3\\\\D\in R \{-2, 3\}\\\\\frac{2}{x+2}-\frac{1}{x-3}=0 /+\frac{1}{x-3}\\\frac2{x+2}=\frac1{x-3}\\2(x-3)=1(x+2)\\2x-6=x+2\\2x-x=2+6\\x=8[/tex]
[tex]c)\\\\\frac{x}{x-1}=\frac{x+2}x\\\\x-1 \neq 0\\x\neq 1\\\\x\neq 0\\\\D\in R/ \{0, 1\}\\\\x^2=(x-1)(x+2)\\x^2=x^2+2x-x-2\\x^2-x^2-2x+x=-2\\-x=-2\\x=2[/tex]
[tex]d)\\\\\frac{x-3}{x-2}=\frac{x+3}{x+2}\\\\x-2\neq 0\\x\neq 2\\\\x+2\neq 0\\x\neq -2\\\\D\in R/ \{-2, 2\}\\\\(x-3)(x+2)=(x-2)(x+3)\\x^2+2x-3x-6=x^2+3x-2x-6\\x^2-x-6=x^2+x-6\\x^2-x^2-x-x=-6+6\\-2x=0 /:(-2)\\x=0[/tex]
[tex]e) \\\\\frac{x+1}x=\frac{x+1}{2x+1}\\\\x\neq 0\\2x+1\neq 0\\2x\neq -1 /:2\\x\neq -\frac12\\D\in R /\{-\frac12, 0\}\\\\x(x+1)=(x+1)(2x+1)\\x^2+x=2x^2+x+2x+1\\x^2+x=2x^2+3x+1\\x^2-2x^2+x-3x-1=0\\-x^2-2x-1=0\\-(x^2+2x+1)=0\\x^2+2x+1=0\\\Delta=2^2-4*1*1=4-4=0\\x_0=\frac{-2}{2}=-1[/tex]
[tex]f)\\\\\frac{x+1}{2x-1}-\frac{2}x=0 /+\frac2{x}\\\frac{x+1}{2x-1}=\frac2{x}\\\\2x-1\neq 0\\2x\neq 1 /:2\\x \neq \frac12\\\\x\neq 0\\\\D\in R / \{0, \frac12\}\\\\x(x+1)=2(2x-1)\\x^2+x=4x-2\\x^2+x-4x+2=0\\x^2-3x+2=0\\\Delta=(-3)^2-4*1*2=9-8=1\\x_1=\frac{3-1}2=\frac22=1\\x_2=\frac{3+1}2=\frac42=2[/tex]
-
Autor:
adan608
-
Oceń odpowiedź:
5
Odpowiedź:
Szczegółowe wyjaśnienie:
a)
4/x = 3/(2 + x) to, najpierw musimy wykluczyć wartość 0 z mianownika,
to: (x ≠ 0 i ∧ 2 + x ≠ 0) to ⇒ (x ≠ 0 ∧ x ≠ - 2) ⇒ D: x ∈ R \ {0; -2}
[Gdzie: koniunkcja zdań (∧ zamiast " i "), jest prawdziwa gdy oba zadnia są prawdziwe, ⇒ wynikanie, implikacja (⇒ zamiast "to"), D: Dziedzina
funkcji: (czytamy): x należy do zbioru liczb rzeczywistych (R) (minus \
zbiór dwuelementowy {0; -2} lub za wyjątkiem zbioru
dwuelementowego {0; -2} ]
4/x = 3/(2 + x) /•x(2 + x) to 4(2 + x) = 3x to 8 + 4x = 3x to
4x - 3x = - 8 to x = - 8 jest rozwiązaniem tego równania.
_________________________________ Sprawdzenie:
Do równania wyjściowego podstawiamy rozwiązanie x = - 8 to
4/x = 3/(2 + x) to 4/(-8) = 3/(2 - 8) to - 1/2 = 3/(-6) to - 1/2 = - 1/2
to Lewa strona równania L = P Prawej, co należało sprawdzić.
b)
2/(x + 2) -1/(x - 3) = 0 to Dziedzina: D: x ∈ R \ {-2; 3}
2/(x + 2) -1/(x - 3) = 0 /•(x + 2)(x - 3) to 2(x - 3) - (x + 2) = 0 to
2x - 6 - x - 2 = 0 to x = 2 + 6 to x = 8 jest rozwiązaniem tego
równania.
Sprawdzenie: L = 2/10 - 1/5 = 1/5 - 1/5 = 0, P = 0 to L = P
co należało sprawdzić.
c)
x/(x - 1) = (x + 2)/x to Dziedzina: D: x ∈ R \ {1; -2}
x/(x - 1) = (x + 2)/x /•x(x - 1) to x² = (x + 2)(x - 1) = x² + 2x - x - 2 to
to x² = x² + x - 2 to x² - x² = x - 2 to x - 2 = 0
to x = 2
Sprawdzenie:
L = 2/(2 - 1) = 2/1 = 2, P = (2 + 2)/2 = 4/2 = 2 to L = P
co należało sprawdzić
-
Autor:
hueyclarke
-
Oceń odpowiedź:
2
Znasz odpowiedź? Dodaj ją tutaj!
Other related questions that may help you
-
Autor:
compton
-
Autor:
probocortez
-
Oceń odpowiedź:
9
-
Autor:
alejo
-
Autor:
zionmosley
-
Oceń odpowiedź:
10