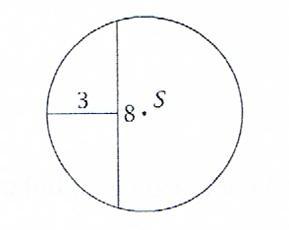
Oblicz promień koła o środku w punkcie S.
-
Temat:
Matematyka -
Autor:
vinny -
Utworzono:
1 rok temu
Odpowiedzi 2
Odpowiedź:
Z tw. Pitagorasa
r²=4²+(r-3)²
r²=16+r²-6r+9
25=6r
r=25/6
r=4 1/6
-
Autor:
romeomthx
-
Oceń odpowiedź:
11
Odpowiedź:
[tex]\huge\boxed{r=\dfrac{25}{6}}[/tex]
Szczegółowe wyjaśnienie:
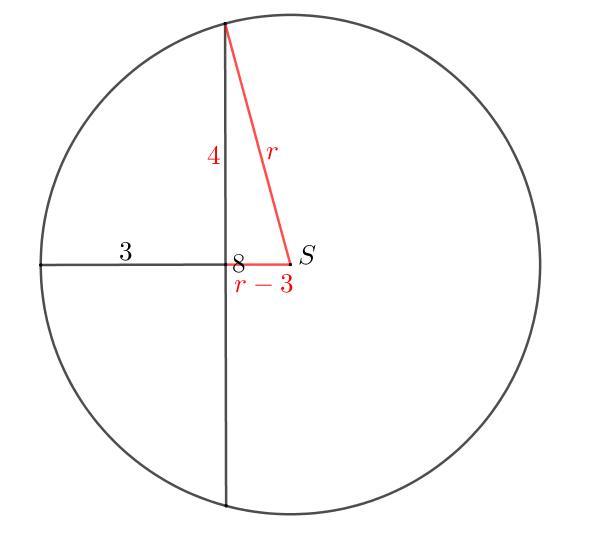
Patrz rysunek w załączniku.
Z twierdzenia Pitagorasa mamy:
[tex](r-3)^2+4^2=r^2[/tex]
skorzystamy ze wzoru skróconego mnożenia
[tex](a-b)^2=a^2-2ab+b^2[/tex]
[tex]r^2-2\cdot r\cdot3+3^2+16=r^2\qquad|-r^2\\\\-6r+9+16=0\\\\-6r=25\qquad|-25\\\\-6r=-25\qquad|:(-6)\\\\\boxed{r=\dfrac{25}{6}}[/tex]
-
Autor:
armanidbcr
-
Oceń odpowiedź:
7
Znasz odpowiedź? Dodaj ją tutaj!
Wybierz język i region
How much to ban the user?
1 hour
1 day
100 years