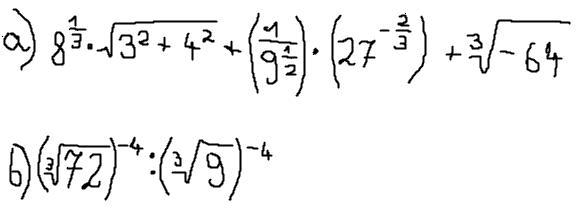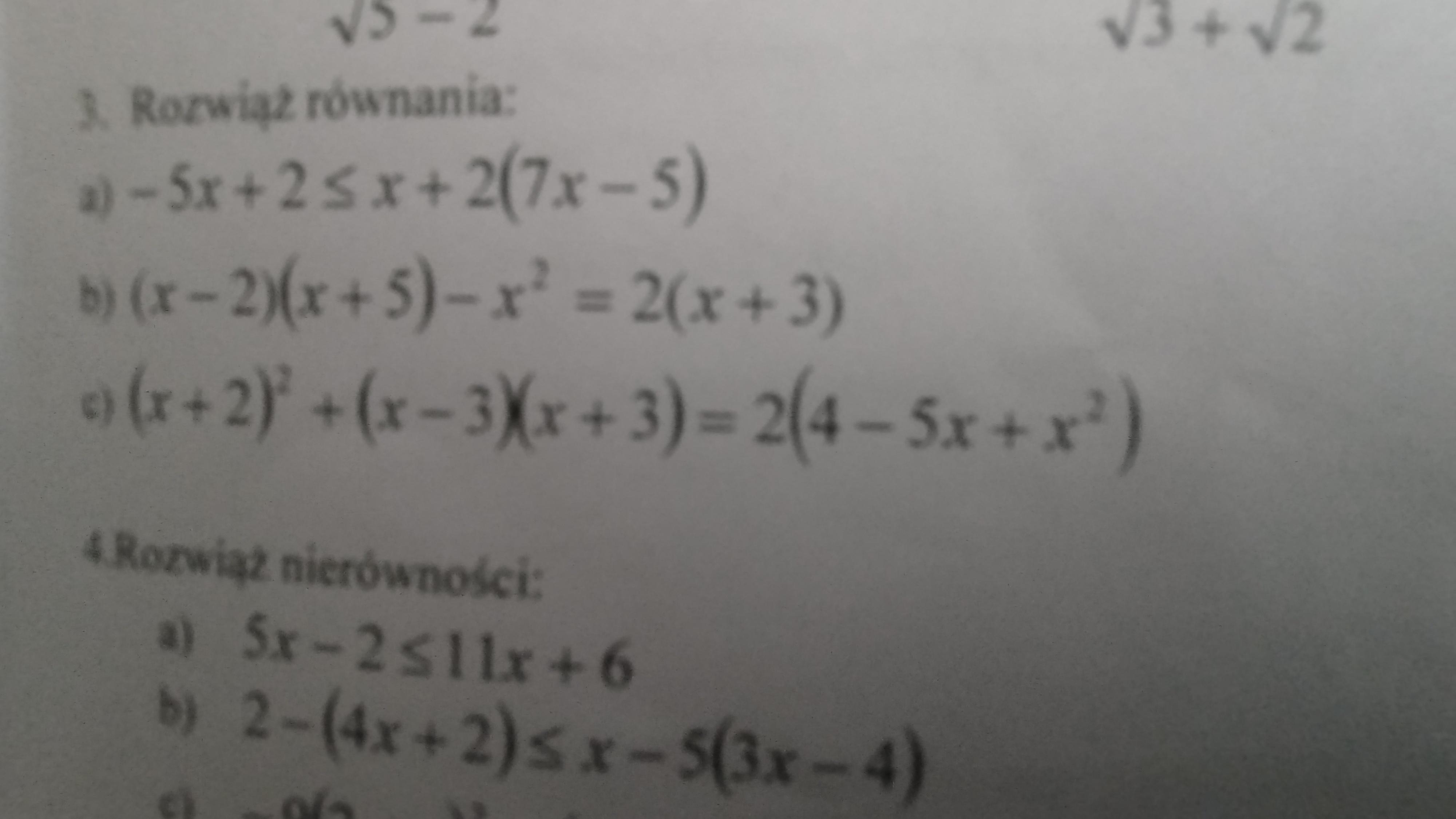a) Porównaj liczby: (załacznik); b) Oblicz odległość między liczbami -6 i 12;

-
Temat:
Matematyka -
Autor:
inés -
Utworzono:
1 rok temu
Odpowiedzi 2
[tex]|\frac{\sqrt{5} }{5} - 1| = 1 - \frac{\sqrt{5} }{5} \\\\|-1,5| = 1,5 \\\\|-1,5| > |\frac{\sqrt{5} }{5} - 1|[/tex]
12 - (-6) = 12 + 6 = 18
:)
-
Autor:
bizzymsdx
-
Oceń odpowiedź:
7
Odpowiedź:
a)
√5 ≈ 2.2
a = | √5/5 - 1 | = | 2.2/5 - 1 | = | 0.44 - 1 | = | -0.56 | = 0.56
b = | -1.5 | = 1.5
więc:
a<b
b>a
b)
| -6 | + | 12 | = 6 + 12 = 18
odp: Odległość między liczbami -6 i 12 wynosi 18.
Szczegółowe wyjaśnienie:
P.S. Z punktem a (porównaj liczby) nie jestem do końca pewien bo dawno tego nie robiłem ale wydaje mi się że jest dobrze
-
Autor:
zaniyahtpy3
-
Oceń odpowiedź:
2
Znasz odpowiedź? Dodaj ją tutaj!
Wybierz język i region
How much to ban the user?
1 hour
1 day
100 years