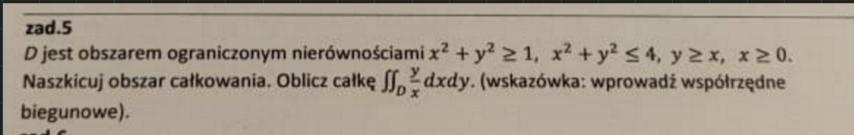Proszę rozwiązać to zadanie.
-
Temat:
Matematyka -
Autor:
thelma -
Utworzono:
1 rok temu
Odpowiedzi 1
Rozwiązanie:
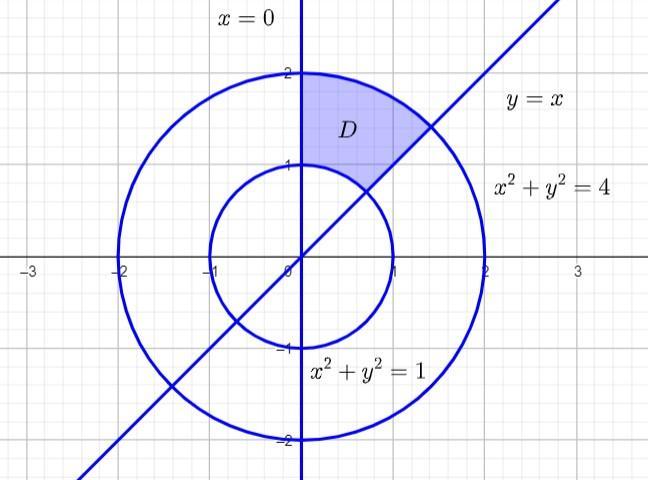
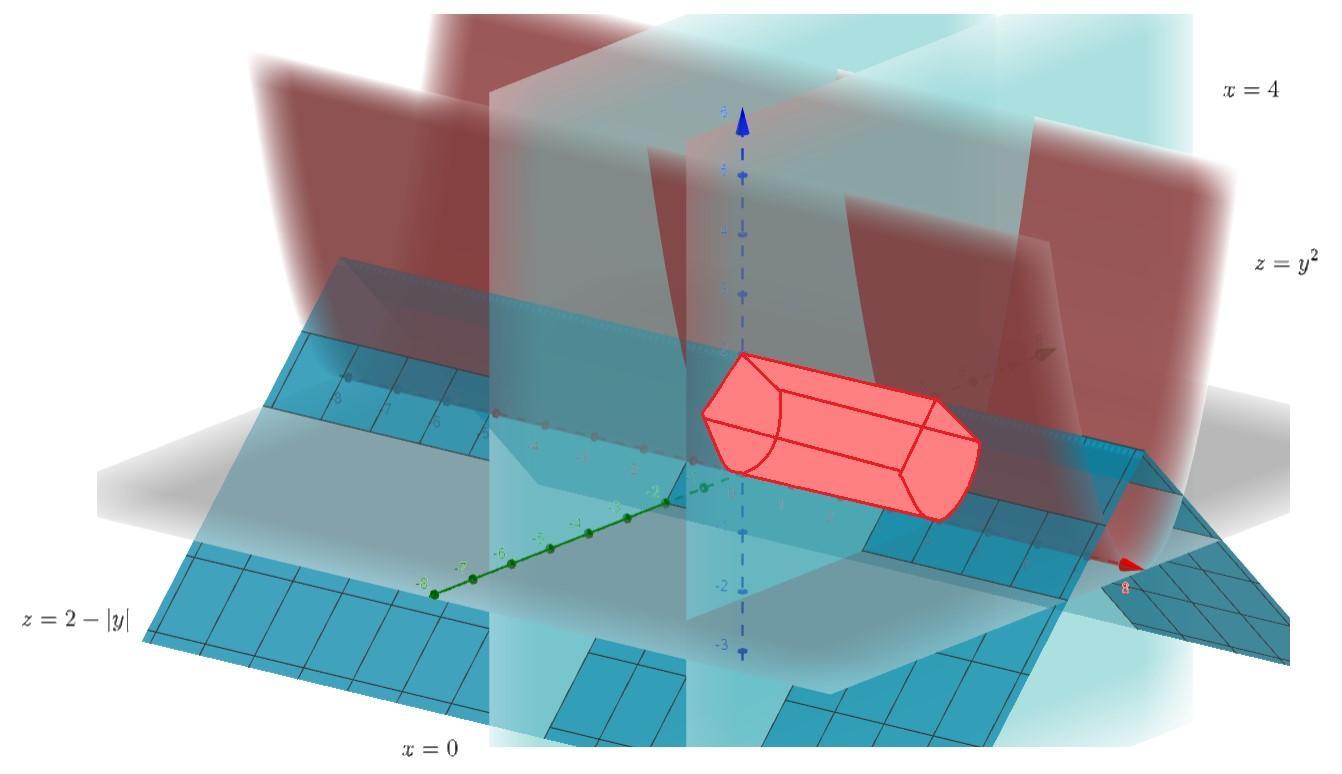
Rysunek w załączniku.
Określenie granic całkowania:
Z polecenia natychmiast dostajemy:
[tex]0\leq x\leq 4[/tex]
[tex]y^{2}\leq z\leq 2-|y|[/tex]
Wyznaczamy granice zmienności [tex]y[/tex] :
[tex]$\left \{ {{z=2-|y|} \atop {z=y^{2}}} \right. \iff2-|y|=y^{2}[/tex]
Korzystając z tego, że [tex]|y|^{2}=y^{2}[/tex] mamy:
[tex]|y|^{2}+|y|-2=0[/tex]
[tex]\Delta=1-4 \cdot 1 \cdot (-2)=9[/tex]
[tex]$|y|=\frac{-1-3}{2}=-2 \ \text{(sprzeczne)}[/tex]
[tex]$|y|=\frac{-1+3}{2}=1[/tex]
[tex]y=-1 \vee y=1[/tex]
Ostatecznie:
[tex]-1\leq y\leq 1[/tex]
Przechodzimy do całki:
[tex]$|V|=\int\limits^{4}_{0} \int\limits^{1}_{-1} \int\limits^{2-|y|}_{y^{2}} dzdydx=\int\limits^{4}_{0}\int\limits^{1}_{-1}\Big(2-|y|-y^{2}\Big)dydx=\int\limits^{4}_{0}\Bigg(\int\limits^{1}_{-1}\Big(2-|y|-y^{2}\Big)dy\Bigg)dx[/tex]
Policzmy osobno wewnętrzną całkę:
[tex]$\int\limits^{1}_{-1}\Big(2-|y|-y^{2}\Big)dy=\int\limits^{0}_{-1}\Big(2+y-y^{2}\Big)dy + \int\limits^{1}_{0}\Big(2-y-y^{2}\Big)dy=[/tex]
[tex]$=2y+\frac{y^{2}}{2}-\frac{y^{3}}{3}\Bigg|^{0}_{-1}+2y-\frac{y^{2}}{2}-\frac{y^{3}}{3}\Bigg|^{1}_{0}=-\Big(-2+\frac{1}{2}+\frac{1}{3}\Big)+2-\frac{1}{2}-\frac{1}{3}=\frac{7}{3}[/tex]
Zatem:
[tex]$\int\limits^{4}_{0}\Bigg(\int\limits^{1}_{-1}\Big(2-|y|-y^{2}\Big)dy\Bigg)dx=\int\limits^{4}_{0}\frac{7}{3} \ dx=\frac{7}{3}x\Bigg|^{4}_{0}=\frac{28}{3}[/tex]
-
Autor:
gerardocarroll
-
Oceń odpowiedź:
3
Znasz odpowiedź? Dodaj ją tutaj!
Other related questions that may help you
-
Autor:
mendoza
-
Autor:
anisevvst
-
Oceń odpowiedź:
5
-
Autor:
kileycraig
Rozwiązanie:
Rysunek w załączniku.
Całka:
[tex]$\iint\limits^{}_{D}\frac{y}{x} \ dxdy[/tex]
Współrzędne biegunowe:
[tex]$\left \{ {{x=r\cos \varphi} \atop {y=r\sin \varphi}} \right.[/tex]
[tex]J(r, \varphi)=r[/tex]
gdzie (patrz rysunek):
[tex]1\leq r\leq 2[/tex]
[tex]$\frac{\pi}{4}\leq \varphi\leq \frac{\pi}{2}[/tex]
Zatem:
[tex]$\iint\limits^{}_{D}\frac{y}{x} \ dxdy=\int \limits^{2}_{1}\Bigg(\int\limits^{\frac{\pi}{2}}_{\frac{\pi}{4}} \frac{r\sin \varphi}{r \cos \varphi} \cdot r \ d \varphi\Bigg)dr=\int \limits^{2}_{1}\Bigg(\int\limits^{\frac{\pi}{2}}_{\frac{\pi}{4}} r\tan \varphi \ d \varphi\Bigg)dr[/tex]
Łatwo zauważyć, że:
[tex]$\int\limits^{\frac{\pi}{2}}_{\frac{\pi}{4}}\tan \varphi \ d \varphi=\lim_{a \to \frac{\pi}{2}} \int \limits^{a}_{\frac{\pi}{4}} \tan \varphi \ d \varphi=\lim_{a \to \frac{\pi}{2}}-\ln \cos \varphi \Bigg|^{a}_{\frac{\pi}{4}}=-\lim_{a \to \frac{\pi}{2}} \Big(\ln \cos a-\ln \frac{\sqrt{2}}{2}\Big)=[/tex]
[tex]$=\ln\frac{\sqrt{2}}{2}-\lim_{a \to \frac{\pi}{2}}\ln \cos a=\ln \frac{\sqrt{2}}{2}-\ln0=\infty[/tex]
Stąd wniosek, że wyjściowa całka jest rozbieżna (objętość pod wykresem funkcji [tex]$f(x,y)=\frac{y}{x}[/tex] na obszarze [tex]D[/tex] nie jest skończona).
-
Autor:
arniescott
-
Oceń odpowiedź:
10
-
Autor:
irene62
Odpowiedź zamieściłem na zdjęciu.
(-_-(-_-)-_-)
-
Autor:
makenzie2onm
-
Oceń odpowiedź:
8
-
Autor:
buster25
Odpowiedź w załączniku.
(-_-(-_-)-_-)
-
Autor:
sugarxwdr
-
Oceń odpowiedź:
5