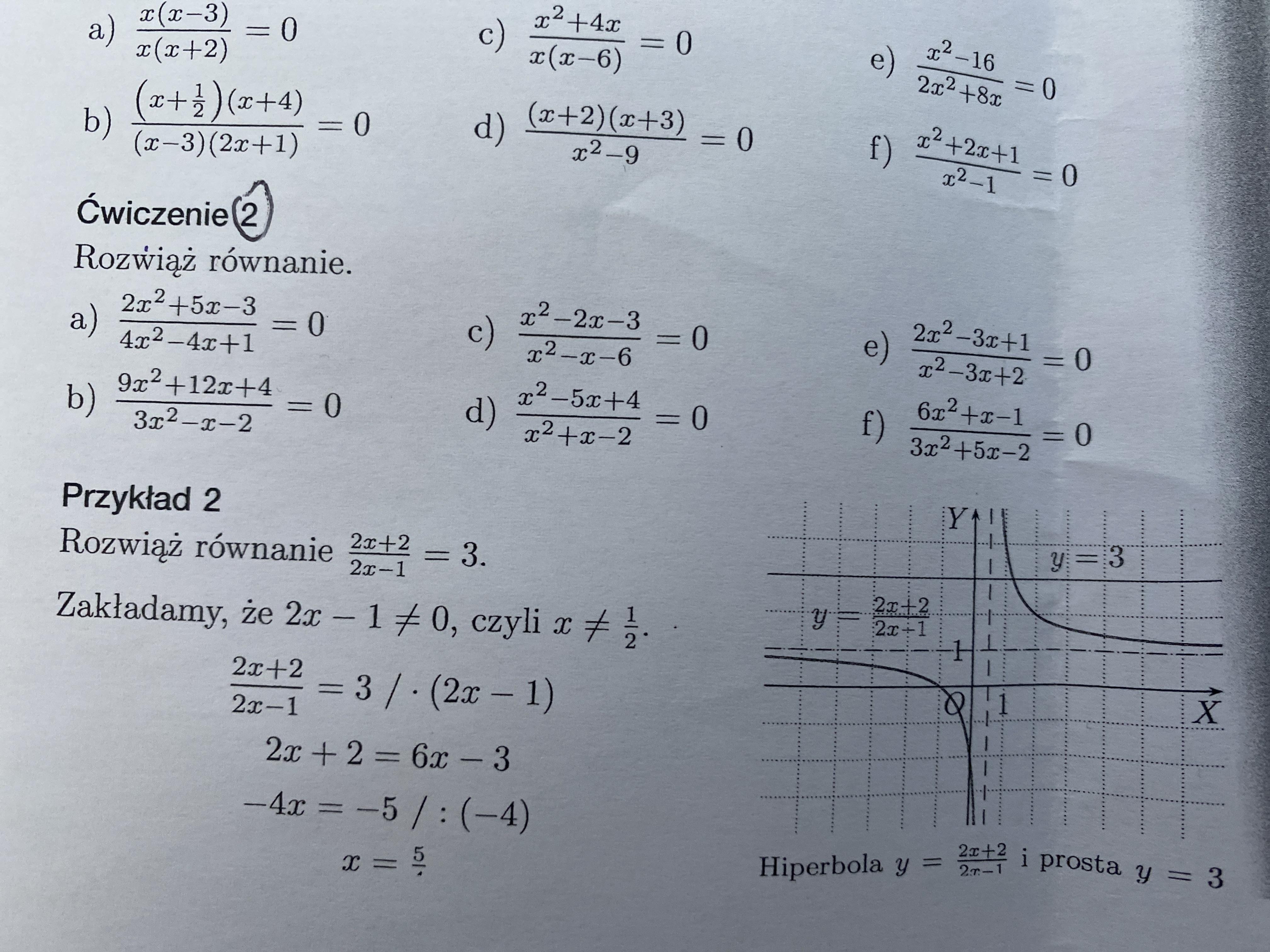Równania wymierne 3.7. Ćwiczenie 1 Rozwiąż równanie.

-
Temat:
Matematyka -
Autor:
alejo -
Utworzono:
1 rok temu
Odpowiedzi 1
[tex]a)\\\\\frac{x(x-3)}{x(x+2)}=0\\\\x(x+2)\neq0\\x\neq 0\\x+2\neq0\\x\neq -2\\\\D\in R \{-2, 0\}\\\\x(x-3)=0\\x=0 \notin D\\x-3=0\\\underline{x=3}[/tex]
[tex]b)\\\\\frac{(x+\frac12)(x+4)}{(x-3)(2x+1)}=0\\\\(x-3)(2x+1)\neq0\\x-3\neq 0\\x\neq 3\\\\2x+1\neq0\\2x\neq -1 /:2\\x\neq -\frac12\\\\D\in R\{-\frac12, 3\}\\\\(x+\frac12)(x+4)=0\\x+\frac12=0\\x=-\frac12 \notin D\\\\x+4=0\\\underline{x=-4}[/tex]
[tex]c)\\\\\frac{x^2+4x}{x(x-6)}=0\\\\x(x-6)\neq 0\\x\neq 0\\x-6\neq 0\\x\neq 6\\\\D\in R \{0, 6\}\\\\x^2+4x=0\\x(x+4)=0\\x=0 \notin D\\\\x+4=0\\\underline{x=-4}[/tex]
[tex]d)\\\\\frac{(x+2)(x+3)}{x^2-9}=0\\\\x^2-9\neq 0\\(x-3)(x+3)\neq 0\\x\neq 3 \text{ v } x\neq -3\\ \\ D\in R \{-3, 3\}\\\\(x+2)(x+3)=0\\x=-3 \notin D\\\underline{x=-2}[/tex]
[tex]e)\\\\\frac{x^2-16}{2x^2+8x}=0\\\\2x^2+8x\neq0\\2x(x+4)\neq0\\\\2x\neq 0\\x\neq 0\\\\x+4\neq 0\\x\neq -4\\\\D\in R \{-4, 0\}\\\\x^2-16=0\\(x-4)(x+4)=0\\x=-4 \notin D\\\underline{x=4}[/tex]
[tex]f)\\\\\frac{x^2+2x+1}{x^2-1}=0\\\\x^2-1\neq 0\\x^2\neq 1\\x\neq 1 \text{ v } x\neq -1\\ \\D\in R \{-1, 1\}\\\\x^2+2x+1=0\\\Delta=2^2-4*1*1=4-4=0\\x_0=\frac{-2}2=-1 \notin D\\\\\underline{\text{Brak rozwiazan}}[/tex]
-
Autor:
zionmosley
-
Oceń odpowiedź:
10